Location: [CPSC 333] [Listing by Topic] [Listing by Date] [Previous Topic] Larger Example
This material was covered during lectures on April 14, 1997.
Z is based on set theory, and many of the definitions and predicates in schemas use operations on sets.
As in computer science, a ``type'' in Z can be thought of as a special kind of set, that includes elements that are similar in some way.
A ``type'' must be defined for each value that is included in a specification written using Z, and the ``type'' is unique - that is, the value belongs to exactly one type.
The only ``standard'' type in Z is the integer type; as shown in the initial example, this denoted by a ``blackboard bold'' Z, just as it frequently is in mathematics lectures and texts.
It's possible to define enumerated types (fixed, finite sets) by assigning names to them and listing their values. For example, the statement
Status ::= registered | passed
defines a new type, ``Status,'' that has two elements called registered and passed, while the statement
Sign ::= positive | zero | negative
defines a new type, ``Sign,'' that has three elements called positive, zero, and negative. The combination of a pair of colons and equality symbol is used to form a type definition operator in Z, as above.
It can also be useful to introduce the name of a type without being precise about the values that it contains. In a basic type definition, the name of a new type (or sequence of new types, separated by commas) is listed by itself in square brackets. For example,
[Student_Name]
declares a new type called Student_Name.
Subsets of types, or ``subtypes'' can also be introduced and used in many of the places where the name of a type would normally appear. For example, the set of natural numbers, consisting of all the integers that are greater than or equal to zero, is a standard subtype in Z (it's a subset of the integers). It's represented by a ``blackboard bold N'', just as it frequently is mathematics lectures and texts. In a schema you could ``declare'' a value x to be an integer:
![]()
However, it should be understood that this declares x to be a value whose type is ``integer,'' that is also required to be a natural number. Thus, you should think of the above axiomatic description as being an ``abbreviation'' for the following one:
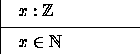
Another useful kind of ``subtype'' of the integers is a range of values. If a and b are integers such that a is less than or equal to b, then
a..b
denotes the set of all integers that are greater than or equal to a and less than or equal to b.
It's possible to introduce names for useful subtypes - or, indeed, for any constants or sets that have already been defined, using a ``definition'' symbol, ==, which is just a pair of ``equality'' signs concatenated together. For example, the declaration
Digit == 0..9
introduces the name Digit for the set of integers between 0 and 9 (inclusive), while you could use the statement
ID_Number_Size == 6
if you wanted to introduce the name ID_Number_Size for the integer constant 6, and then use the name (instead of the constant value itself) elsewhere in the specification.
If S and T are sets, then the Cartesian product of S and T,
![]()
contains all the ordered pairs whose first elements belong to S and whose second elements belong to T.
In Z, unusual notation is used to represent ordered pairs. If s is an element of S and t is an element of T then
![]()
is used to represent the element of the Cartesian product of S and T with first element s and second element t, instead of the more common notation, (s, t).
In these notes, the more common notation (s, t) will sometimes be used, just to make it easier to present this material using the web.
Z provides operators called first and second that can be used to extract the components of an ordered pair, which work the way their names should suggest. For example,
first((s, t)) = s, and second((s, t)) = t
If S and T are types (as well as just ``sets'') then the Cartesian product of S and T is a type, as well.
If S is a set, then the power set of S,
![]()
is the set of all the subsets of S. For example, if the type Sign is as given above, then the power set of Sign would include the following values (each of which is a subset of Sign):

The first value listed above is the empty set (as it's written in Z specifications).
The standard operations on sets - union and intersection, as well as the comparisons and ``is a subset of,'' ``is a superset of,'' etc all written in Z in the same was they generally are in mathematics lectures and texts. (At least) one other operation is useful: If S is a finite set, then
#S
denotes the number of elements in S (which is often written as ``|S|'' in mathematics lectures and texts, instead).
If S and T are sets then a binary relation between S and T is a (sub)set of ordered pairs whose first elements belong to S and whose second elements belong to T. Note that this definition agrees with the definition generally used in mathematics (although, it may have been a while since you've seen it).
Thus, if S and T are types then a binary relationship between S and T is something whose type is
![]()
Since this type often arises in specifications, it has a shorter name:
![]()
That is, another way to write the type ``Binary relationships between S and T'' is by using S, followed by a horizontal double-headed arrow, followed by T.
If r is a binary relation between S and T, then the domain of r is the set of elements s of S such that there is at least one ordered pair (s, t) in r for some element t of T. The range of r is the set of elements t in T such that there is at least one ordered pair (s, t) in r for some element t of T.
In Z, the domain and range of r are written as
dom r
and
ran r
respectively.
Consider, for example, the following relation r from the integers to the integers.
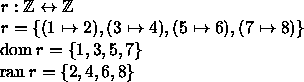
If r is a binary relation from S to T, and s1 is a subset of S, then the domain restriction of r to s1 is the set of ordered pairs in r whose first coordinates belong to s1. This is also a binary relation from S to T, and it is written as
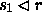
Similarly, if r is as above and t1 is a subset of T, then the range restriction of r to t1 is the set of of ordered pairs in r whose second coordinates belong to t1. This is a binary relation from S to T as well, and it is written as
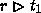
In particular, if r is as above, then
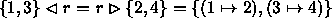
If r is a binary relation from S to T, and s2 is a subset of S, then the domain exclusion from r of s2 is the set of ordered pairs in r whose first elements do not belong to s2. This binary relation from S to T is written as
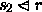
Similarly, if r is a binary relation from S to T, and t2 is a subset of T, then the range exclusion from r of t2 is the set of ordered pairs in r whose second elements do not belong to t2. This binary relation from S to T is written as
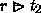
In particular, if r is as above, then
![]()
If S and T are types, then partial functions from S to T and total functions from S to T are particular kinds of binary relations from S to T. A partial function from S to T is a binary relation from S to T such that, for every element s of S, there is at most one element t of T such that (s, t) is in the relation, while a total function from S to T is a binary relation from S to T such that, for every element s of S, there is exactly one element t of T such that (s, t) is in the relation.
Thus, the set of all partial functions from S to T, and the set of all total functions from S to T, are both ``subtypes'' of the set of binary relations from S to T, and one is a proper subset of the other (every total function is a partial function, but the converse is not true). The set (or subtype) of partial functions from S to T is written as
![]()
while the set (or subtype) of total functions from S to T is written as
![]()
While the choice of notation may seem odd, note if we declare f to be a total function from S to T, using the notation given above, then we'll end up using a statement that's identical to what you'd write in mathematics - f, followed by a colon (:), followed by the name of the ``subtype'' (S, followed by an arrow, followed by T, as given above).
If f is a partial (or total) function from S to T, and x is an element of S, then you can write ``the result of applying f to x'' exactly as you would in mathematics:
f(x)
However, the brackets are considered to be optional in Z, so you could write
f x
as well. (It may be difficult to see, but there is a space between f and x in the above line.) By default, functions are ``prefix'' operators, but you can define ``infix'' and ``postfix'' operators as well (see the references for Z that have already been given for more information).
Now suppose that r1 and r2 are both partial functions from S to T. Then another partial function, written as
![]()
can be defined from both. This is the partial function whose domain is the union of the domains of r1 and r2, such that if x is in the domain of r2 then the function's value at x is r2(x); if x is in the domain of r1 but not r2 then the function's value at x is r1(x), and such that the function is not defined at x otherwise.
For example, if r is as above then r a partial function from the integers to themselves, and
![]()
Once again, let's consider Version One of the Student Information System.
We'll begin by defining types for the attributes of the entity ``Student.''
To shorten this example slightly, we'll use a single attribute, called ``Student_Name'' instead of the three attributes for first name, middle initial, and last name used in the original version of this example. We'll show that ID numbers are integers, simply introduce ``Student_Name'' as a named type, and we'll introduce ``Status'' as an enumerated set:
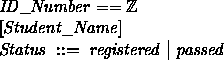
Now, a schema can be written to define allowed states for the entity ``Student.'' As this example shows, you can often represent an entity (which corresponds to a table of data) as a partial function from the entity's key to non-key data. Cartesian products can be used if either the key or the non-key data includes more than a single attribute.

Recall that, in Z, partial functions are just special kinds of relations, and relations are just special kinds of sets. We can ``initialize'' the ``Students'' data area by setting the (final version of the) partial function it includes to be the empty set:
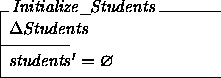
Once again, partial functions are just special kinds of sets. Thus, we can use ``set union'' to extend the domain of a function, as shown below: This schema adds one more ordered pair (formed from the inputs) to the partial function - defining it for one more value in the domain - if the input really does correspond to a new student; it leaves the function (and the data area) unchanged, otherwise. An output, outcome!, is used to report which case occurred.
Note the inspection of the domain of the partial function, in order to decide whether a change is necessary.

One of the ``Update'' operations specified in the problem description is to be used to show that a student - who is currently registered in the course - has now passed it. The following schema specifies such an operation. It uses several of the pieces of notation defined above, including function application and the use of the operator ``second'' in order to confirm that the specified students is currently registered in the course, and the use of a function override to make the required change.

Another desired ``Update'' operation could be used to correct a student's name, as an exercise, try to write a schema that checks whether a request for a change should be made, makes it (if appropriate), and reports the outcome.
A desirable ``deletion'' operation is one that processes a student's withdrawal from the course. Note that the following schema is very similar to the one given above: It needs to make exactly the same error checks as above. In this case, though, it uses domain exclusion (or ``domain subtraction'') to make the required change, instead of function override.

If you want to try additional exercises, then you could try to extend this example by writing schemas for the additional functions mentioned in the problem description. Another (probably less interesting) exercise would be to replace the named type, Student_Name, used above, by three types for First_Name, Middle_Initial, and Last_Name, and make the changes needed to the above schemas so that they agree more completely with the original description of the problem.
Another good exercise might be to try to develop definitions and schemas for Version Two of the Student Information System, instead of Version One. In this case, you'd probably need to use a binary relation (instead of a partial function) in order to represent the ``relationship'' that's included in this example. You'd also need to include predicates relating domains and ranges of the binary relations and partial functions you've used, in order to define a ``class invariant'' for the class(es) you specify.
It's hoped that these examples have given you an idea of what formal specifications (written in Z) look like. However, there's additional useful material about specifications in Z that these notes haven't covered.
Refer to any of the books already listed in these notes for information about additional components of the language that haven't been used here, and for some information about how you might use formal methods for other parts of system development besides requirements analysis and specification.
For some additional information about such things as tool support, and object-oriented extensions of the language, see the Z home page.
Location: [CPSC 333] [Listing by Topic] [Listing by Date] [Previous Topic] Larger Example