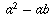Dividing by zero!

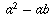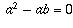This is the oldest fallacy in the book: to "cancel" a quantity from both sides of an equation is to divide both sides of the equation by it. So, in this step of the proof we are attempting to divide both sides of the equation by (IMAGE) .  However, division only makes sense when the number you are dividing by is non-zero. In this proof, (IMAGE) , because we assumed in step 1 that a=b!

Therefore, it makes no sense to divide both sides of the equation by 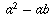(IMAGE) , because that would be dividing by zero.

In essence, this proof boils down to saying "1 times 0 equals 2 times 0, therefore 1 equals 2". The fallacy is that, just because two numbers give you the same answer (zero) after you multiply them each by zero, doesn't necessarily mean that the two numbers are the same, because anything when multiplied by zero gives zero.

This is also the reason division by zero does not make sense: there isn't just one unambiguously determined number q such that 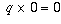(IMAGE) , so there isn't any number that we can uniquely and unambiguously define the quotient 0/0 to be.

If you tried to divide 1 (or some other non-zero number) by 0, you'd run into a different problem: in this case, there is no number q at all such that 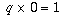(IMAGE) , so there is nothing that we can define the quotient 1/0 to be.

That's why division by zero is undefined (not just because it's a rule somebody decided on!)