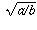 equal
equal 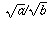 ?
? 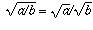 is quite wrong! Well ... except in the case in
which a and b are both positive.
is quite wrong! Well ... except in the case in
which a and b are both positive.
If this surprises you, think about the question
Why shouldIf you were to try to convince someone of this, you'd have to start with the definition of what a "square root" is: it's a number whose square is the number you started with. So, from first principles, all that has to be true is thatequal
?
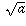 squared is a,
squared is a, 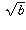 squared is b, and
squared is b, and 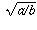 squared is a/b.
squared is a/b.
So, when you square 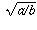 , you will get a/b, and when you square
, you will get a/b, and when you square 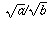 , you will also get a/b. That's all that the definition of
square root tells you.
, you will also get a/b. That's all that the definition of
square root tells you.
Now, the only way two numbers x and y can have the same square is if x = +/- y. So, what is true is that
but in general there's no reason it has to be,
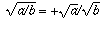 rather than
rather than 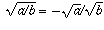 , unless a and b are both positive: for then (because
by convention we take the positive square root) everything in the above
equation is positive, and that's why we obtain
, unless a and b are both positive: for then (because
by convention we take the positive square root) everything in the above
equation is positive, and that's why we obtain 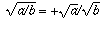 . But remember it's only because everything is positive that we obtain it!
. But remember it's only because everything is positive that we obtain it!
In our case, it is true that 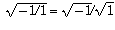 , but
, but 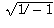 is
is 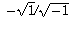 not
not 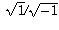 . The fallacy comes from using the latter instead of the former.
. The fallacy comes from using the latter instead of the former.
In fact, the whole proof really boils down to the fact that (-1)(-1) =
1, so 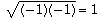 , but
, but 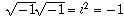 (not 1). The proof tried to claim that these two were equal (but in a more
disguised way where it was harder to spot the mistake).
(not 1). The proof tried to claim that these two were equal (but in a more
disguised way where it was harder to spot the mistake).
This fallacy is a good illustration of the dangers of taking a rule from
one context and just assuming it holds in another. When you first learned
about square roots you had never encountered complex numbers, so the only
objects that had sqare roots were positive numbers. In this case, 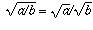 is always true, and you were probably taught it as a "rule". But it is
only a mathematical truth in that original context, and fails to remain true
after you extend the definition of "square root" to allow the square roots
of negative and complex numbers.
is always true, and you were probably taught it as a "rule". But it is
only a mathematical truth in that original context, and fails to remain true
after you extend the definition of "square root" to allow the square roots
of negative and complex numbers.