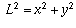The fallacious step was the first step!

There is the implicit assumption here that the top of the ladder remains resting against the wall. However, that is not always true. Once the ladder has reached a sufficiently small angle to the horizontal, your pulling of the bottom away from the wall will actually cause the top to pull away from the wall too. When this happens, there is no longer the relationship (IMAGE)

, because x, y, and L no longer form the sides of a closed right triangle.

If you want to verify this for yourself, just try it out on your favourite ladder. You will see that the top pulls away from the wall just before the ladder becomes horizontal.

To understand mathematically (or rather, physically) why this is true, suppose for a moment that there was no gravity. Then, when you pull the ladder, you will pull the entire ladder as a unit, with both top and bottom moving away from the wall with the same speed.

A good exercise is to try to figure out the equation for the position of the top of the ladder during this free-fall stage.