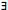" is provided as a shorthand for the cardinality constraint "
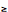1".
Brian R Gaines
Knowledge Science Institute
University of Calgary, Alberta, Canada
gaines@ucalgary.ca
Description logics are valuable for modeling the conceptual structures of scientific and engineering research because the underlying ontologies generally have a taxonomic core. Such structures have natural representations through semantic networks that mirror the underlying description logic graph-theoretic structures and are more comprehensible than logical notations to those developing and studying the models. This article reports experience in the development of visual language tools for description logics with the objective of making research issues, past and present, more understandable.
Scholarship may be conceptualized as the rational reconstruction of intuitive notions within the conventions of a discipline. When scholarly disciplines examine their foundations the outcome is generally a taxonomy based on logical definitions intended to capture the concepts of the primary researchers and to clarify the differences underlying disagreements. The development and analysis of such taxonomies can be helpful to active research communities attempting to clarify their activities, and it is also significant in retrospect to historians reconstructing the conceptual structures of those recognized as major contributors to the growth of human knowledge. Description logics managed through visual languages isomorphic to the underlying graph-theoretic structures, and visually transformable through well-defined deductive processes, offer an attractive technology to support both historic studies and active research communities.
The work reported in this paper is a continuation of that on the use of knowledge acquisition and representation tools to model the knowledge structures of scholarly communities [1]. These studies involved the use of the visual language [2] that allowed knowledge structures to be expressed as semantic networks with well-defined semantics that were automatically translated into data structures in KRS [3], an implementation of a CLASSIC-like [4] description logic. Inferences in KRS were graphed automatically as additions to the semantic network so that users could visualize both the inputs and outputs without translation into logical formulae [5].
In recent years there have been major advances in description logic research that make it realistic to use richer representations incorporating negation, disjunction and some aspects of recursion [6]. This enables one to overcome of the artificiality of the knowledge structures noted above that attempted to avoid such constructions, resulting in unnatural representations, of lesser use as models meaningful to the relevant community.
This paper reports on recent developments that: extend the visual language to support richer description logics with disjunction, negation and existential quantification; exemplifies the process of transforming semantic networks in coming to understand them; discusses factoring deduction into its intensional and extensional operations to support paraconsistent reasoning [7]; and raises a number of issues for future research.
I have used the term "understanding an ontology" in order to capture the notion that users should be able to see the effects of variations in the ontology, some of which do not change its meaning, others of which change it significantly in ways that can be readily understood, and others of which are logical consequences that may require some degree of explanation if they are to be understood.
A visual language representation of ontologies is useful to support those without great fluency in symbolic logic in its textual representation. Shin [8] has demonstrated that diagrammatic reasoning can provide a rigorous foundation for logical inference, and psychological experiments show that non-technical users of a knowledge-based system find inference in a visual language easier to understand [9].
The design criteria for the visual language have been:
KNet, the visual language used in this paper is implemented in a generic visual language shell, RepNet [12], that supports a user-specified syntax for node types and connecting lines and a user scriptable interface for translation to and from semantic networks in the visual language enabling integration with web services such as KRS and RACER [13]. It is simple to change the language to conform to existing practices, user preferences, or changing notions of what is required. The examples given follow the conventions described in [2] and are similar to those of other graphical interfaces for description logics such as RICE [14].
Concepts are represented by the concept name in an oval. Concepts are defined through the property they encode [15] in the graph derived by tracing outgoing arrows from the concept, terminating at concept nodes or terminal nodes. Concepts are used through incoming arrows, and may be both defined and used in the same graph.
Base, or primitive, concepts are indicated by short horizontal markers in the concept oval that indicate that there is some unspecified outgoing graph unique to the concept. This is a sufficient explication (in Carnap/Quine terms [16]) for the logical properties of a primitive concept. From a logical perspective, is does not matter in reasoning with the concept how the unspecified graph is represented provided it is unique to the concept. However, in modeling scientific reasoning, one has to take into account that each school of thought may have adopted a differing, more specific representation of a particular primitive concept, making a distinction without a difference that can be a source of confusion in the literature.
Roles, or relations, are represented by the role name without any surrounding shape.
Individuals, or singletons, are represented by the individual name in a rectangle. An individual exhibits [15] a property derived from its outgoing arrows as for concepts, which may be conceptualized as the concept encoding its current state.
A collective individual or set is represented by an extensional constraint, and possibly an
identifying name, in a rectangle with inset vertical lines at each end. The
constraint is specified through upper and lower cardinality and inclusion
bounds on the collection as detailed in [3] where it was shown that such bounds
may be conceptualized as defining generalized sets or mereological collections
having well defined unions, intersections and complements, and forming a
subsumption lattice under inclusion ordering (I have not yet found an elegant
graphical representation of the bounds, and hence have left these defined in
textual form within the node). Sets are important in representing role fillers,
co-reference and inclusion constraints, and, when defined by comprehension,
material implications or rules. The notation for an individual may be regarded
as a shorthand for a set with cardinality 1 (consistent with the Quine/Scott
[17/18] extensional simplification of set theory that a={a}). Thus there are
basically only three types of nodes: concepts, roles and mereological sets. The node type "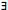" is provided as a shorthand for the cardinality constraint "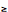1".
Arrows between nodes derive their semantics from the types of the nodes they connect.
An arrow from concept A to concept B means that concept A is defined to be subsumed by concept B. The equivalent graph-theoretic interpretation is that the arrow may be replaced by copying the graph of outgoing arrows from concept B to concept A (including the unspecified graph of a primitive concept).
An arrow from individual A to concept B means that A is asserted to be an instance of B and again may be given a graph-theoretic interpretation as a copy operation.
An arrow from an individual A or a set A to a set B means that A is contained in B. This can be used to specify co-reference and inclusion constraints. An arrow from a concept A to a set B means that any individual comprehended by A is contained in B. This has the corollary that a rule, or material implication, may be represented as a set with a incoming arrow from a premise concept and an outgoing arrow to a conclusion concept.
Multiple arrows from a node are taken as specifying a conjunction of properties. This convention necessitates the
introduction of a special node, "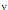
", specifying a disjunction, with the convention that outgoing arrows from this
specify a disjunction of properties. The graph-theoretic interpretation is one
of multiple alternative graphs each having one of the branches of the
disjunction, and disjunction nodes can always be eliminated by such expansion
resulting in multiple, alternative definitions of a disjunctive concept.
The conjunctive node type "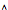
" is also available to use after a "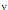" to disambiguate multi-branch outgoing graphs that
are to be treated as a single term in the disjunction.
Negation is represented through an arrow with a cross bar having the graph-theoretic interpretation that the graph at the end of the arrow must not occur. This gives rise to the standard semantics for negation, including De Morgan's laws linking conjunction, disjunction and negation. A negation arrow from a concept to a set may be used to represent a rule with exceptions [19].
An existential constraint is specified through a set with an arrow to a concept applying to the individuals included in it.
If a graph contains a conjunction/disjunction of two identical graphs then one of the conjuncts/disjuncts may deleted.
A concept definition is coherent, or consistent, if all the set bounds specified in it are consistent and there is no conjunction in it of an arrow and a negation arrow pointing to the same graph.
A model satisfying an ontology defined in the visual language is a collection of individuals satisfying all the existential constraints such that their resulting states are coherent.
One ontology is extensionally subsumed by another if any model satisfying it also satisfies the other. This definition gives rise to the standard denotational, extensional, model-theoretic semantics for description logics, and may be used to show that the graph-theoretic operations of the visual language conform with the standard extensional semantics of description logics.
We may also introduce the notion of intensional or structural subsumption as a sub-graph relation, that one ontology is intensionally subsumed by another if that other ontology is a sub-graph of it. It follows immediately that intensional subsumption implies extensional subsumption, but not necessarily vice versa.
However, the definition of intensional subsumption needs strengthening. First, a semantic network may be conceptualized as a meta-graph that specifies a set of equivalent graphs derivable from it by expansion, contraction and other logical operations. One ontology intensionally subsumes another if its graph at any stage of expansion or contraction is a sub-graph of the other at any stage of expansion or contraction. One could state this in terms of full expansions to a canonical form but for computational purposes the definition given is more useful, particularly since recursive definitions give rise to infinite graphs.
Second, the labels given to non-primitive concepts are arbitrary from a logical perspective, so that any remapping of labels that preserves non-identity may be used in computing structural subsumption. This corresponds to the notion that different terms are being used for the same concept, and is important in the analysis of scientific definitions since it often happens that different terminology has been used for essentially the same concept. Mapping primitives to one another is a deeper operation since it would imply that their tacit definitions are the same, and is also important to the process of finding explications of the primitives. A good example is the way in which the application of biological evolutionary theory to processes in other disciplines has led to the abstraction of the principles of variety generation and selective filtering underlying a general process of 'evolution.'
Third, the semantics of set constraints have not been specified in graphical form, but their subsumption lattice is well-defined so that one needs to extend the notion of sub-graph to be one in which a set matches another if it subsumes it.
In order to illustrate some of the issues, this section takes the following simple ontology from The Description Logic Handbook [6, p.52] and shows how it may be manipulated in KNet.
Woman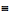 
Person 
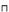Female (1)
Man 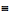Person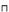 
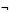Woman (2)
Mother 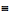Woman 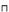has_Child.Person (3)
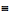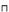Father Man has_Child.Person (4)
Parent 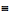Father 
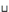Mother (5)
Grandmother 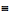Mother 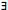has_Child.Parent (6)
Mother_With_Many_Children 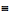Mother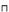 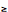3 has_Child (7)
Mother_Without_Daughter 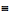Mother 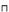has_Child.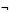Woman (8)
Wife 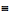Woman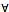 
has_Husband.Man (9)
Figure 1 Simple ontology of family relationships [6, p.52]
Fig.2 shows the ontology of Fig.1 represented as a semantic network in KNet.
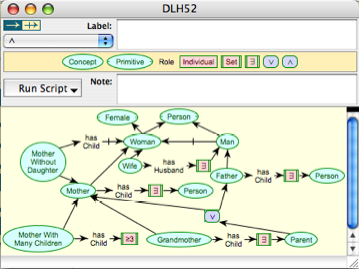
Figure 2 Ontology of Figure 1 in KNet
Figure 3 is equivalent to Figure 2, and derived from it by expanding all defined constructs, pushing negation to terminal nodes, and excising contradictory branches from disjunctions. These are all transformations that a representation system will probably make in transforming the definitions into an internal normal form, and they are also of help to the user in understanding the ontology.
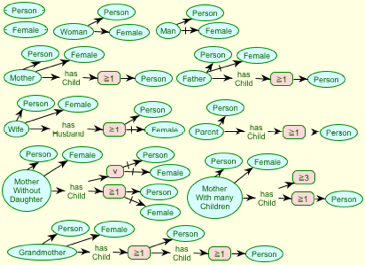
Figure 3 Expanded ontology of Figure 2
Some problems with the ontology defined in Figure 2 are apparent in Figure 3. "Mother Without Daughter" and "Mother With Many Children" are not defined as expected because they encompass situations in which a child is not a person. The problem may be viewed as arising from the definition of "Mother" that has "Person" after an existential quantifier, and it could be avoided by moving "Person" back to be a universal quantifier of the "has Child" role. However, this would have the consequence in recognizing a "Mother" that all her children would have to be checked to be people when it is intended that only the existence of one need be checked.
These problems are arising because the ontology of Figure 2 avoids the use of the natural recursive definition that the "has Child" role of a person must be filled by a person. However, this is an innocuous use of recursion since the concept "Person" is a primitive that can only be asserted of an individual, not recognized as applying to it, and hence the recursive definition acts only as a constraint that needs propagating through a graph up to its existing terminal nodes, not expanded indefinitely beyond them.
Fig. 4 shows an alternative ontology with the recursive definition, and Fig. 5 shows that it leads to the expected definitions after expansion.
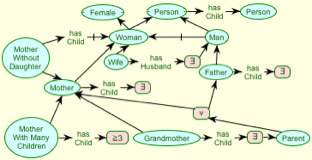
Figure 4 Alternative ontology to Figure 1
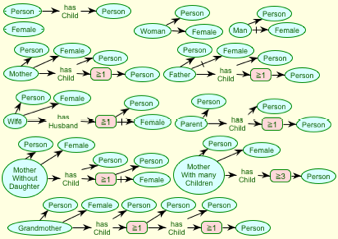
Figure 5 Expanded ontology of Figure 4
Fig. 5 looks somewhat cluttered with "Person" terminals, and the user might wish to limit the expansion by specifying that those implicit in the recursive definition are not shown, in effect that the "has Child" role of a person is implicitly filled by a person. Nine uses of "Person" can be dropped in Fig. 5 while preserving its equivalence to Fig. 4.
The point of this discussion to illustrate how various transformations of a ontology may affect the understanding of it, and need to be supported through decision logic inference and graphical interaction. Users need to be able to move back and forth between readily understood equivalent representations, much as does the inference engine. It is interesting to see how the defined subsumptions in Fig.4 are clearly visible to users as inferable subsumptions in Fig. 5 through subgraph relationships. Users also need to be able to compare the effects of changes that do affect meaning such as those between Fig.2 and Fig.4.
The situation becomes more complex as inferences are made that go beyond the restructuring discussed so far, for example, if it is the A-Box that is being graphed and extensional case-by-case reasoning has been applied or rules have fired. KRS graphs the results of such reasoning as additions as to the original graph after "infer" nodes, but makes no attempt to "explain" them. CLASSIC provides a form of explanation of terminological reasoning [20] and this together with more recent developments [21,22] suggest approaches which it would be interesting to implement as modules providing graphical output through semantic networks.
In its applications to presenting output from clustering algorithms, KNet provides an interactive interface whereby users can adjust what parts of a graph are shown by moving a slider to change a threshold. It would be interesting to take output from an inference engine in a proof markup language [23] and have a slider that moved through a linear representation of the proof steps while showing the resulting inferences being graphed in the semantic network.
Figure 6 provides a simple example of the distinctions made in Aristotle's mechanics that led to problems that medieval scientists attempted to resolve with little progress until their reconstruction by Galileo facilitated their explication by Newton [24]. The state of an object was seen to be either one of rest or one of motion, and several states of motion were distinguished. One that was well-grounded in experience but problematic in the development of a unified science of motion, was the distinction between heavenly and local bodies. The problems generated by this distinction without a difference were greatly exacerbated by making circular, constant motion part of the definitional essence of heavenly motion, thus requiring no explanation in terms of material conditionals or 'laws of motion.'
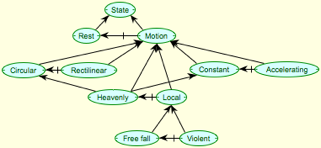
Figure 6 Distinctions in medieval mechanics
Medieval scientists accepted the heavenly—local distinction and the lack of need to explain the 'perfection' of heavenly motion, and focused on problems with the behavior of bodies in free-fall motion, that they accelerated, and ones in 'violent' motion, such as projectiles, that they continued in the direction in which they were projected even though they had lost contact with the projector. This led to explanations in terms of notions such as impressed 'impetus' [24].
Galileo dropped the distinction between heavenly and local bodies and between free fall and violent motion, but introduced new problems through the notion that the earth itself was moving and yet this had no apparent effect on objects in free fall. One can track the changing ontologies and laws from Aristotle through Buridan and Oresme to Copernicus and Galileo and hence to Descartes, Huygens, Hooke, Newton et al, as the gradual reduction of primitives in the ontologies of motion and their replacement by the material implications which we now know as Newton's 'laws of motion' [24].
One important phenomenon in the development of scientific reasoning is the way in which qualitative distinctions become refined to be graded distinctions, eventually becoming numeric scales of observable measured with ever-increasing precision [25]. We can model this process in a description logic by introducing the natural symmetry of an opposition, that it is generally conceived as based on two opposing concepts of equal status rather than one and its negation as in Figs. 2, 4 and 6. The resultant structure turns out to have the properties of a multi-point scale.
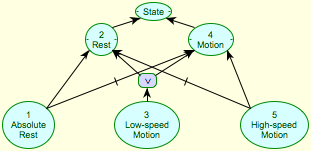
Figure 7 From an opposition to a five-point scale
Fig. 7 exemplifies this process. The opposition between the primitives, rest and motion, is modeled by the extremes of absolute rest and high-speed motion which inherit from one concept and the negation of the other. This leads to a natural five-point scale as three other concepts are interpolated between them, the two primitives and their disjunction. Seven and nine-point scales may be developed from this by adding another concept such as 'extreme value.' Once the logical possibility of grading the opposition has been realized it is natural to look for quantities to measure that correlate with the scale and provide further gradations.
In the literature on modeling scientific reasoning it has been argued that inconsistencies are often present but do not cause "explosive" growth of conclusions through the ex falso quodlibet derivations of classical logic [7]. Hence it has been proposed that paraconsistent logics are needed to account for scientific reasoning [26]. However, uniform paraconsistency is not desirable since many major achievements in the scientific literature, such as Arrow's impossibility theorem, result from proofs of definitional inconsistency, and Rips' psychological studies show that people readily generate reductio ad absurdum arguments to solve logic problems [27].
Batens has proposed and developed adaptive logics that default to classical behavior in the absence of inconsistency, but behave paraconsistently in its presence [28]. Description logics are well-suited to be foundations for such logics if the reasoning is factored appropriately. The major example of ex falso quodlibet in description logics is that any incoherent definition is subsumed by any other. However, structural subsumption based on graph-matching does not lead to this conclusion. It has to be imposed separately. KRS [3] would happily report that a Meinongian green, round, square entity, where round and square were declared disjoint primitives, was subsumed by green, round or square but not by red, provided that the additional inference step of noting that the definition was incoherent and mapping it to bottom was not taken.
Tableaux proofs by refutation obviously rely on such mapping but extensions to tableaux methods have been described which support inconsistency-adaptive logics [29] and it would be interesting to investigate how these might be incorporated in description logics.
A reasonable target architecture might be an inference engine with a user-interface through semantic networks and control over the proof methods such that one can see the impact of various methods in terms of the proofs generated and the inferences made. Normalization and structural subsumption might provide a model of the inference patterns that have led to incoherent definitions being accepted by scholarly communities for long periods of time, with inferences being made despite the contradictions. Stronger proof methods might provide a model of the anomaly detection that leads to a change in the conceptual framework marking a minor or major "scientific revolution."
Description logic technology, with visual language interfaces and control of proof techniques, provides very valuable tools for understanding the knowledge processes of current and past scholarly communities. Much of the current research on the support of the semantic web is directly applicable since the sub-disciplines of science are known to form a "semantic web" of inter-dependencies and provenances. It may be that some additional constructions will be needed, but the advances of recent years in description logic research make it reasonable to expect that it will be feasible to add them.
[1] Brian R Gaines and Mildred L G Shaw. Using knowledge acquisition and representation tools to support scientific communities. In Proc. of the 12th Nat. Conf. on Artificial Intelligence (AAAI'94), pages 707-714 1994.
[2] Brian R Gaines, An interactive visual language for term subsumption languages. In Proc. of the 12th Int. Joint Conf. on Artificial Intelligence (IJCAI'91), pages 817-823, 1991.
[3] Brian R. Gaines. A class library implementation of a principled open architecture knowledge representation server with plug-in data types. In Proc. of the 13th Int. Joint Conference on Artificial Intelligence (IJCAI'93), pages 504-509, 1993.
[4] A. Borgida, A., R. J. Brachman, D.L. McGuiness and L.A. Resnick. CLASSIC: a structural data model for objects. In Proc. of SIGMOD Conference on the Management of Data, pages 58-67, 1989.
[5] Brian R Gaines and Mildred L G Shaw. Embedding formal knowledge models in active documents. Communications of the ACM 42(1): 57-63, 1999.
[6] Franz Baader, Diego Calvanese, Deborah McGuinness, Daniele Nardi, and Peter F. Patel-Schneider, editors. The Description Logic Handbook: Theory, Implementation and Applications. Cambridge University Press, 2003.
[7] Walter A. Carnielli, Marcello E. Coniglio and Itala M. Loffredo D'Ottaviano (Eds.). Paraconsistency: The Logical Way to the Inconsistent. New York, Marcel Dekker, 2002.
[8] Sun-Joo Shin. The logical status of diagrams. Cambridge University Press, 1994.
[9] John T. Nosek and Itzhak Roth. A comparison of formal knowledge representations as communication tools: predicate logic vs semantic network. International Journal of Man-Machine Studies 33, 227-239, 1990.
[10] Alex Borgida and Peter F. Patel-Shneider. A semantics and complete algorithm for subsumption in the CLASSIC description logic. Journal of Artificial Intelligence Research 1, 277-308, 1994.
[11] Brian R Gaines. A situated classification solution of a resource allocation task represented in a visual language. Int. J. Human-Computer Studies 40(2): 243-271, 1994.
[12] Rep IV Manual. Centre for Person-Computer Studies, 2004, http://repgrid.com.
[13] Volker Haarslev and Ralf Mšller. Description of the RACER System and its Applications. Proc. of the Int. Workshop on Description Logics (DL-2001), pages 132-141, 2001.
[14] Ralf Mšller, R. Cornet and Volker Haarslev. Graphical Interfaces for Racer: Querying DAML+OIL and RDF Documents. Proc. of the Int. Workshop on Description Logics (DL-2003), 2003.
[15] Edward N. Zalta. Intensional Logic and the Metaphysics of Intentionality. Cambridge, MA: MIT Press, 1988.
[16] Willard Van Orman Quine. Word and Object. Cambridge, MA: MIT Press, 1960.
[17] Willard Van Orman Quine. Set theory and its logic. Cambridge, MA: Harvard University Press, 1963.
[18] Dana S. Scott. Quine's individuals. In Ernest Nagel,Patrick Suppes and Alfred Tarksi (Eds.) Logic, Methodology and the Philosophy of Science. Stanford, CA: Stanford University Press, pages 111-115, 1962.
[19] Brian R Gaines. Integrating rules in term subsumption knowledge representation servers. In Proc. of the 9th National Conference on Artificial Intelligence (AAAI'91), pages 458-463.
[20] Deborah L. McGuiness and Alex Borgida. Explaining subsumption in description logics. In Proc. 14th Int. Joint Conf. on Artificial Intelligence (IJCAI'95), pages 816-821, 1995.
[21] S. Schlobach and R. Cornet. Explanation of Terminological Reasoning: A Preliminary Report. Proc. of the Int. Workshop on Description Logics (DL-2003), 2003.
[22] Deborah L. McGuinness and Paulo Pinheiro da Silva. Infrastructure for Web Explanations. In Proc. of 2nd Int. Semantic Web Conference (ISWC2003), LNCS 2870, Berlin: Springer, pages 113-129, 2003.
[23] Paulo Pinheiro da Silva, Deborah L. McGuinness and Richard Fikes. Combinable Proof Fragments for the Web. Tech. Rep. KSL-03-04, Knowledge Systems Laboratory, Stanford University, 2003.
[24] Eduard Jan Dijksterhuis. The Mechanization of the World Picture. Oxford: Clarendon Press, 1961.
[25] M. Norton Wise (Ed.). The Values of Precision. NJ: Princeton University Press, 1995.
[26] Joke Meheus (Ed.). Inconsistency in Science. Dordrecht: Kluwer, 2002.
[27] Lance J. Rips. The Psychology of Proof: Deductive Reasoning in Human Thinking. Cambridge, MA: MIT Press, 1994.
[28] Diderik Batens, Chris Mortensen, Graham Priest and Jean-Paul Van Bendegem. Frontiers of Paraconsistent Logic. Baldock, UK: Research Studies Press, 2000.
[29] Diderik Batens and Joke Meheus. A Tableau Method for Inconsistency-Adaptive Logics. In Proc. Automated Reasoning with Analytic Tableaux and Related Methods (TABLEAUX 2000), LNCS 1847, Berlin:Springer, pages 127-14, 2000.