| Quicksort |
About This Exercise
The objective of this exercise is to ensure that you understand the QuickSort algorithm well enough to be able to describe this algorithm, trace its execution by hand on small examples, and accurately describe its worst-case and expected performance.
Students should read through and try to solve the problems on this exercise before attending the tutorial on Monday, November 22.
Expected Background
This is based on the lecture on QuickSort that was presented on Friday, November 19. Additional information about this sorting algorithm is available in Secton 11.2 of the textbook and on the Wikipedia page on this topic.
Warmup Problems — To Check That You Understand the Basics
It is expected that all of the questions in this first section can be answered by any student who has successfully completed the prerequisites for this course, and attended the lecture in which QuickSort was discussed (reviewing the onine notes, as needed).
These warmup problems will not be discussed in the tutorial; students who do have difficulty with them should contact the course instructor to get extra help.
-
Briefly describe what each of the following algorithms are supposed to do, as well as how they do it.
- Deterministic Partitioning — DPartition
- Deterministic Quicksort — Quicksort
- Randomized Partitioning — RPartition
- Randomized Quicksort — RQuicksort
-
Consider the following array.
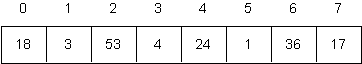
-
Trace the execution of the “Deterministic Partitioning” algorithm on this input. That is, trace the execution of the program after the call
DPartition(A, 0, 7)
if A is the array that is shown above.
-
Notice that this is the first stage of the application of the deterministic Quicksort algorithm to sort the above array.
Trace the rest of the application of this algorithm to sort this array. In order to answer this question you should list each of the following.
- the calls that are made to DPartition after this
- the array before each of these calls is made
- the array after each of these calls is completed
-
-
Repeat the above question, using the following array instead of the one that is shown above.
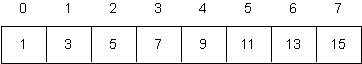
What is notable (and unfortunate) about the lengths of arrays that must be recursively sorted as this algorithm proceeds?
-
Repeat the first question, using the following array instead of the ones that are shown above.
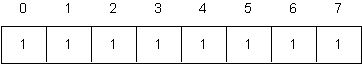
What is notable about the lengths of arrays that must be recursively sorted this time?
What would happen if the randomized version of Quicksort was applied to this array? Why?
To Be Discussed in the Tutorial
-
If you completed the above questions then you may have noticed the following: Neither the deterministic nor the randomized algorithms that have been described in class and in the textbook work particularly well on arrays that include many copies of the same input entry.
-
Modify the DPartition algorithm so that it reorders the input algorithm in much the same way as before. However, the algorithm should now move all copies of the pivot element x into the middle of the part of the array that is being processed, and it should return a pair of integers i and j, on inputs A, p, and r, such that the following properties are satisfied.
-
p ≤ i < j ≤ r+1.
-
For an integer h, if p ≤ h < i then A[h] < x.
-
For an integer h, if i ≤ h < j then A[h] = x.
-
For an integer h, if j ≤ h ≤ r then A[h] > x.
Then modify the proof of correctness and efficiency of the DPartition algorithm to show that your new algorithm is correct and efficient as well.
-
-
Describe a modified version of the deterministic Quicksort algorithm that uses your new partitioning algorithm, and that has better performance when the input array includes many copies of the same algorithm.
-
Make similar modifications to the randomized algorithm. Explain why the resulting algorithm can be expected to perform well on all input arrays.
-
-
We have now considered the worst-case analysis of a deterministic version of Quicksort as well as a a randomized version of the algorithm. This question concerns an average-case analysis of the deterministic version of the algorithm. That is, it concerns the “expected running time” of the deterministic algorithm, assuming a given distribution of the possible inputs.
Notice, again, that it is only the relative order of inputs that effect the running time of the deterministic Quicksort. In this question we will assume that the entries of the input array are distnct so that, for the purpose of this analysis, we may assume that the input array A includes the entries 1, 2, … n arranged in some order, for n = A.length.
-
Here is (perhaps) the most challenging part of the problem. Suppose that the entry i is initially stored at the end of the array, so that — following the first use of DPartition — the entries of A will consist of the integers between 0 and i−1 (in some order), followed by i, followed by the integers between i+1 and n (in some order).
Suppose that each of the (n−1)! initial orderings of the values ahead of i in the input array are equally likely. Use this to show that, after the first application of DPartition, each of the (i−1)! relative orderings of the initial i−1 values is equally likely, and each of the (n−i)! relative orderings of the last n−i values is equally likely, as well.
-
Use the above information, along with the analysis of the randomized version of the algorithm (which must now be modified) to prove the following:
If each of the n! initial relative orderings of the array entries is equally likely, then the expected cost to sort an array A of length n using the deterministic version of Quicksort is in O(n log n).
-
-
As some of the above may suggest, we know how how to modify either the deterministic or randomized version of the Quicksort algorithm in order to improve their worst-case performance. Yet the simple versions (with terrible worst-case performance) tend to be implemented and used?
Why?
Additional Problem (To Be Discussed if Time Permits)
-
Here is another way to modify Quicksort so that it works well on inputs with multiple copies of the same element. Unfortunately the version presented here does not sort in place, so that it requires additional storage.
This version of the algorithm will not modify its input. It will access and modify a second array L, where it is initially the case that L[i] = i for each integer i such that 0 ≤ i < A.length.
The entries of A are not changed in any way as this version of the algorithms is used — the entries of L are instead, so that, at each point during the computation,
A[L[0]], A[L[1]], A[L[2]], …, A[L[A.length−1]]
is the sequence of values (in order) that would be found in A using the original version of the algorithm.
Of course the array L will generally not be sorted — but it can be used to produced the array that would be obtained by sorting A when the algorithm terminates.
-
Trace the execution of the modified algorithm on the array shown in Question #2, above.
-
Now consider using the extra information that is now available to redefine the ordering that is being use in order to break ties: In particular, if we comparing values A[L[i]] and A[L[j]], where i is not equal to j, then
- if A[L[i]] < A[L[j]] according to the ordering that we have been using so far, then A[L[i]] < A[L[j]] using the new ordering as well.
- if A[L[i]] > A[L[j]] according to the ordering that we have been using so far, then A[L[i]] > A[L[j]] using the new ordering as well.
- finally, if A[L[i]] = A[L[j]] according to the ordering that we have been using so far, then A[L[i]] < A[L[j]] using the new ordering if i < j (using the usual ordering of integers) and A[L[i]] > A[L[j]] if i > j.
Confirm that if Quicksort is applied using the “new” ordering, then this can be used (quite quickly) to produce the array that would be obtained from A by sorting it using the “old” ordering.
-
Use the above to describe a version of randomized Quicksort whose expected cost to sort any array of length n is in O(n log n).
-
|
Last updated:
http://www.cpsc.ucalgary.ca/~jacobs/cpsc331/F10/tutorials/tutorial18.html |