Tutorial 23, CPSC 331, Winter 2012

home page -  news -  syllabus -  schedule -  assignments -  tutorials -  tests -  java -  references -  Mike Jacobson

Tutorial 1 -  Tutorial 2 -  Tutorial 3 -  Tutorial 4 -  Tutorial 5 -  Tutorial 6 -  Tutorial 7 -  Tutorial 8 -  Tutorial 9 -  Tutorial 10 -  Tutorial 11 -  Tutorial 12 -  Tutorial 13 -  Tutorial 14 -  Tutorial 15 -  Tutorial 16 -  Tutorial 17 -  Tutorial 18 -  Tutorial 19 -  Tutorial 20 -  Tutorial 21 -  Tutorial 22 -  Tutorial 23

 Computation of Minimum-Cost Spanning Trees

About This Exercise

The objectives of this exercise are

Please read through and try to solve the problems on this exercise before attending the tutorial.

Background and Preparation

This exercise is baded on information about minimum-cost spanning trees, and an algorithm that can be used to find them, presented in lectures on Prim's Algorithm.

Warmup Problems — To Check That You Understand the Basics

It is expected that all of the questions in this first section can be answered by any student who has successfully completed the prerequisites for this course and attended the lectures on the computation of minimum-cost spanning trees was introduced (reviewing the online notes, as needed).

These warmup problems will not be discussed in the tutorial; students who do have difficulty with them should contact the course instructor to get extra help.

  1. Define the cost of a spannning tree in a connected weighted undirected graph G. Then define a minimum-cost spanning tree in G.

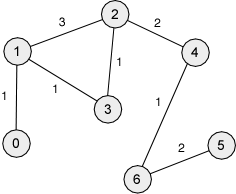
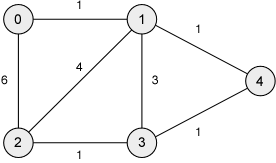
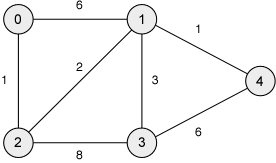
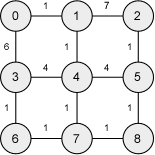
  2. Trace the execution of MST-Prim on the following weighted undirected graphs. In order to obtain the same as executions, you should choose 0 as the start vertex and visit neighbours of each vertex by increasing value for the label.

    1.  

      A Weighted Graph

    2.  

      Another Weighted Graph

    3.  

      Yet Another Weighted Graph

    4.  

      A Final Weighted Graph
       

  3. What would happen if you applied Prim’s algorithm to a weighted graph G that is not connected? What, if anything, could be stated and proved about the algorithm’s output in this case?

  4. Prove the following claim, which was used in the proof of correctness of both Dijkstra’s and Prim”s algorithms.

    Claim: Suppose that each vertex in an undirected graph is coloured either white, grey, or black. Suppose, as well, that every neighbour of a black node is black, as well. Then the only vertices that are reachable from any black nodes are also black.

  5. Compare and contrast each of the following.

    1. a set of minimum-cost paths from a start vertex to other vertices, and a minimum-cost spanning tree
    2. Dijkstra’s algorithm and Prim’s algorithm

To Be Discussed in The Tutorial

  1. For the analysis of the graph algorithms that have been studied during the last few weeks of classes, it has been assumed that it is possible to enumerate the set of neighbours of a given vertex v using time that is linear in the number of neighbours, that is, linear in the degree of this vertex.

    One of the two common representations of graphs supports an enumerations of the neighbours of a vertex at this cost, while the other does not.

    1. Which of the two common representations of a graph can be used to perform this operation, at this cost?
    2. What is the cost to traverse the set of neighbours of a given vertex if the other common graph representation is used, instead? Why?
    3. Give the best asymptotic upper bound, that you can, for the number of steps that would be used by Prim’s algorithm, in the worst case, to find a minimimum-cost spanning tree of a connected, weighted, undirected graph G = (V, E), if this other representation was used to represent the input graph G.

  2. Consider either Dijkstra’s algorithm to compute minimum-cost paths, or Prim’s algorithm to compute a minimum-cost spanning tree. Suppose that either is applied to some weighted, connected undirected graph G = (V, E) and vertex s.

    1. Try to find the best upper bound on the number of times that each of the following operations is performed on a Min-Heap, when either of these algorithms is applied.

      • Insert
      • Minimum (which reports the element with minimal priority without removing it)
      • DeleteMin
      • Decrease-Priority

      Hint: You should find that one of these operations can be performed significantly more often than any of the rest.

    2. A Fibonacci heap is another data structure that can be used to implement a priority queue. While the worst-case of operations is greater than those for a binary heap, the amortized cost of a sequence is actually better: The total cost of any sequence of operations beginning with an empty heap, that includes p Insert, Minimum and Decrease-Priority operations and q DeleteMin operations is in O(p + q log n), if n is the maximum size of the priority queue during this sequence of operations.

      Use this information to give an asymptotic upper bound (in terms of |V| and |E|) on the number of steps used in the worst case, by either Dijkstra’s algorithm or Prim’s algorithm, if the binary heap used by the algorithm is replaced with a Fibonacci heap.

    3. For which graphs (or kinds of graphs) would versions of the algorithms using Fibonacci heaps be asymptotically faster than versions using binary heaps?

Last updated:
http://www.cpsc.ucalgary.ca/~jacobs/Courses/cpsc331/W12/tutorials/tutorial23.html