Tutorial 19, CPSC 331, Winter 2012

home page -  news -  syllabus -  schedule -  assignments -  tutorials -  tests -  java -  references -  Mike Jacobson

Tutorial 1 -  Tutorial 2 -  Tutorial 3 -  Tutorial 4 -  Tutorial 5 -  Tutorial 6 -  Tutorial 7 -  Tutorial 8 -  Tutorial 9 -  Tutorial 10 -  Tutorial 11 -  Tutorial 12 -  Tutorial 13 -  Tutorial 14 -  Tutorial 15 -  Tutorial 16 -  Tutorial 17 -  Tutorial 18 -  Tutorial 19 -  Tutorial 20 -  Tutorial 21 -  Tutorial 22 -  Tutorial 23

 Term Test 2 Review

About This Exercise

This exercise can be used by students as part of their efforts to prepare for Term Test #2, which will be written at 5:00pm, in SB 142, on Monday, March 26.

Students should work thorugh this exercise — preferably by having studied ahead ahead of time and having used this as a time-limited “practice test” before attending the tutorial that day.

Expected Background

It is expected that students have studied the material introduced in this course following the material assessed since Term Test #1 — beginning with lecture material on trees, binary trees and binary search trees, and ending with material on quicksort

Sample Problems

Problems like the following ones have appeared on the second term test in this course in the last few years.

There is, of course, no guarantee that similar ones will be used again this year — but they do test your understanding and ability to apply the material that is to be assessed on the upcoming term test, and they are reasonable test questions.

  1. Consider a regular binary search tree T.

    1. Give pseudocode for an algorithm that can be used to search for the node with a given key in the binary search tree T.

    2. Say briefly how you would prove that the algorithm you have described, above, is correct.

    3. State the worst-case cost of this algorithm as a function of the depth of T.

    4. State the worst-case cost of this algorithm as a function of the size of T.

    5. Draw the binary search tree T that would be obtained by deleting the node with key 8 from the following binary search tree.

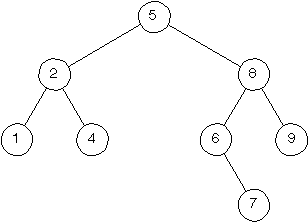
      A Binary Search Tree

  2. Consider the red-black tree data structure.

    1. State the definition of the black-height of a node in a red-black tree.

    2. State the red-black properties that must be satisfied by any binary search tree (with nil nodes added as leaves) that is also a red-black tree.

    3. How is the depth of a red-black tree related to its size?

    4. State the worst-case cost to insert a new value into a red-black tree as a function of the size of the tree. Is this better than, the same as, or worse than the worst-case cost for this function when it is performed on a regular binary search tree with the same size?

  3. Consider hashing with open addressing, using table size m=8, using the following hash function to choose an intial value to store,

    h(x) = x mod 8

    and using linear probing for collision resolution.

    1. Draw the hash table (with the above table size and hash function) that would be produced by inserting the following values into an initially empty hash table.

      1, 11, 12, 3, 40

    2. How many operations to used to search for an element in a hash table (with open addressing, using linear probing for collision resolution, and with table size m) in the worst case, if the hash table stores n values?

      What does the hash table look like when this “worst-case number of operations” is actually used?

      You may asymptotic notation to give your answer.

    3. Searches in a hash table are frequently considerably less expensive than the worst-case analysis of the operations would suggest. An average-case analysis of the performance of hashing algorithms supports this claim.

      Discuss this “average-case analysis.” If you can, you should include

      • an assumption that is often used to perform an “average-case analysis” of the cost of operations on hash tables with open addressing,

      • the expected number of operations used to perform the operation discussed in part (b) of this question, if the above assumption is correct, and

      • what this average-case analysis implies — if anything — if this assumption is not correct.

      as part of your answer.

  4. Consider algorithms to sort a given array of length n.

    1. Breifly describe an algorithm (using simple English or pseudocode) that can be used to merge two sorted arrays together, producing a sorted array including the entries of both inputs, and using a number of operations that is linear in the sum of the lengths of the input arrays in the worst case.

    2. Give pseudocode for the MergeSort algorithm. You may use the “merging” algorithm, discussed in part (a), as a subroutine without defining or describing it again.

    3. How many operations are used by the MergeSort algorithm to sort an array of length n in the worst case? You may use asymptotic notation to give your answer.

    4. Trace the execution of MergeSort on the following array.

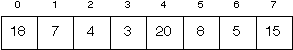
      An Array

    5. How many operations are used to sort an array of length n using Selection Sort in the worst case? Is this asymptotically faster, slower, or the same as MergeSort in the worst case?

Last updated:
http://www.cpsc.ucalgary.ca/~jacobs/Courses/cpsc331/W12/tutorials/tutorial19.html