Tutorial 10, CPSC 331, Winter 2017

Algorithms for Searching

About This Exercise

The objectives of this exercise are

to ensure that you understand the definitions of the searching problems that were discussed;
to ensure that you understand the algorithms for searching included in these lectures. You should be able to
- trace the execution of these algorithms by hand on small examples,
- explain what these algorithms do, both by giving simple English descriptions and providing pseudocode for them,
- understand the proofs of correctness and efficiency of these algorithms, and
- understand and be able to apply the results that were presented about the worst-case running times of these algorithms;
to ensure that you could implement these algorithms by writing Java programs for them (and, ideally, writing programs using other programming languages as well).

Please reaad through and try to solve the problems on this exercise before attending the tutorial.

Expected Background

This exercise is based on material presented during the lecture on searching.

Warmup Problems — To Check That You Understand the Basics

It is to be expected that all of the questions in this first section can be answered by any student who has successfully completed the prerequisites for this course, and attended the lecture in which algorithms for searching were discussed (reviewing the online lecture notes, as needed).

Students who do have difficulty with these questions should contact the course instructor to get extra help.

Give a brief description, in simple English, of each of the following algorithms — saying what problem each solves, and how it solves it.
1. linear search in an unsorted array
2. linear search in a sorted array
3. binary search
Consider the following array A.

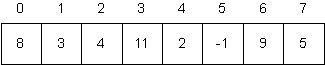
Trace the execution of the Linear Search algorithm when it is used to search for each of 2, 5, and 7 in this array.
Consider the following sorted array A.
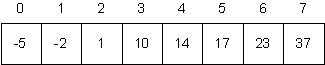
1. Trace of the execution of the Linear Search algorithm for the original Searching Problem, when it is used to search for each of 1, 37, −6, 12, and 38 in this array. That is, show what happens if you search for these values and you do not know that (or take advantage of the fact that) this is a sorted array.
2. Repeat the above question, using the Linear Search algorithm for a sorted array, instead.
3. Repeat the above question, using the Binary Search algorithm instead.
  
  In order to be better prepared for the longer questios at the end of this exercise you should keep track of the values of high and high each time the bsearch subroutine is called, and you confirm that one of the preconditions for this subroutine is satisfied every time it is called.
Consider the problem of “Searching in a Sorted Array,” and the version of the “Linear Search” algorithm that is given for this problem (this is the second of the three algorithms presented in the lecture notes). In this question, you are being asked to make sure that you can fill in the details that were not included in the online notes, so that you can verify the claims about the algorithm that were made.

Consider the loop invariant that is given for the loop in this algorithm.
1. After an inspection of the code, explain why the loop invariant is satisfied immediately before for the first execution of the loop body, if the loop body is executed at all.
2. Let j be a nonnegative integer such that the loop body is executed at least j times.
  
  Suppose the loop invariant is satisfied just before the j^th execution of the loop body. Show that if the loop body is executed and the loop test succeeds, so that the loop body should be executed again, then the conditions in the loop invariant are all satisfied immediately before the j+1^st execution of the loop body, as well.
  
  Verify that this implies that the conditions in the loop invariant are all satisfied immediately before the j^th execution of the loop body (if the loop body is executed j or more times) for every nonnegative integer j. (In other words, this is really is a “loop invariant,” as this has been defined in this course.)
3. Now suppose that the loop body is executed j times but there is not a j+1^st execution of the loop body — because the condition in the loop test is false after the j^th execution of the loop body.
  
  Use the loop invariant to to argue that if i ≥ A.length at this point, then A[h] < k for every integer h such that 0 ≤ h ≤ A.length−1.
  
  Then use the loop invariant to argue that if i < A.length and A[i] ≠ k, then A[k] > k so that, in fact,
  - A[h] < k for every integer h such that 0 ≤ h < i, and
  - A[h] > k for every integer h such that i ≤ h ≤ A.length−1.
4. Use all the above to establish the partial correctness of this linear search algorithm.
5. Finally, show that the function f(A, i) = A.length − i is a loop variant for the loop in this algorithm.
  
  Use this to show that if the algorithm is executed when either one of its preconditions is satisfied then it does eventually terminate (so that the algorithm is also correct), and that the number of steps used by the algorithm is linear in the size of the input array, in the worst case.

To Be Discussed in the Tutorial

Now consider the behaviour of the Binary Search algorithm when it is given a value key to search for and it is being used to search in a sorted array A with positive length n.

Consider, also, the specification of requirements for the bsearch subroutine that is given in the lecture notes.
1. Confirm that the one of the preconditions for the subroutine is satisfied whenever the subroutine is called by the main algorithm (with low = 0 and high = n−1), if A is a sorted array with length n.
2. Confirm that the preconditions for the bsearch subroutine each imply that key is not an element of the array A if high = low−1. (Why is that?)
3. Confirm that the each of the preconditions implies that if low = high then either A[low] = key or key is not an element of the array at all. (Why?)
4. Use the above to argue that if bsearch is called with either of its preconditions satisfied, and with low ≥ high, then bsearch produces the output it should: The corresponding postcondition is satisfied on termination of the algorithm, because the algorithm returns an index h such that A[h] = key if key is an element of the array, and it throws a notFoundException otherwise.
5. Now consider the more interesting case that low < high. Notice that the subroutine might call itself recursively in this case.
  
  Argue that if either one of the subroutine’s preconditions is satisfied when the algorithm is called, and the algorithm then calls itself recursively, then the same precondition is still satisfied — and the array A and value key have not been changed — at the beginning of the recursive call that is made.
  
  This claim is not entirely trivial, because the values for low and high that are mentioned in the preconditions now refer to the first and second inputs supplied to bsearch during this next recursive call (that is, low and mid−1, respectively, in one case, and mid+1 and high, respectively, in another case).
  
  Suppose that the outputs received by this “next” recursive application are correct. After an inspection of the code, confirm that the “current” application of the bsearch subroutine will produce the output that it should, as well.
  
  This can all be used to establish the partial correctness of the Binary search algorithm.
Continue to consider the Binary Search algorithm and the bsearch subroutine that does all the work.
1. Suppose the subroutine is called with (the first two) inputs low and high such that
  
  high = low + 2h − 1
  
  for some positive integer h, so that the part of the array that remains to be searched has length high − low + 1 = 2h.
  
  Show that if bsearch calls itself recursively, then it does to so search a part of the array that has length at most h.
2. Suppose, instead, that bsearch is called with inputs low and high such that
  
  high = low + 2h,
  
  for a positive integer h, so that the part of the array that remains to be searched has length 2h + 1.
  
  Show that if bsearch calls itself recursively, then it does so to search a part of the array that has length at most h in this case, as well.
3. Notice that if bsearch is called when low = high (to search a part of an array with length one) then it calls itself at most once more.
4. Use all of the above to show that if the Binary Search is run on an array of length n, for n ≥ 1, then the total number of calls made to bsearch is at most log₂n + 2.
Now consider the use of Binary Search to search for a key in an array A with positive length n, when the key is greater than all of the values stored in A Use mathematical induction to show that bsearch is called at least log₂ n + 1 times during this search.
Use the results of the last three questions to argue that the Binary Search algorithm is correct and, furthermore, that it can be used to search in a sorted array of length n using Θ(log₂n) operations in the worst case.

Last updated:
http://www.cpsc.ucalgary.ca/~jacobs/Courses/cpsc331/W17/tutorials/tutorial10.html