Tutorial 15, CPSC 331, Winter 2017

Tutorial 1 -  Tutorial 2 -  Tutorial 3 -  Tutorial 4 -  Tutorial 5 -  Tutorial 6 -  Tutorial 7 -  Tutorial 8 -  Tutorial 9 -  Tutorial 10 -  Tutorial 11 -  Tutorial 12 -  Tutorial 13 -  Tutorial 14 -  Tutorial 15 -  Tutorial 16 -  Tutorial 17 -  Tutorial 18 -  Tutorial 19 -  Tutorial 20 -  Tutorial 21 -  Tutorial 22 -  Tutorial 23 -  Tutorial 24

Red-Black Trees

About This Exercise

The objectives of this exercises are

• to ensure that you understand the definition and basic properties of a red-black tree;
• to ensure that you understand operations on red-black trees well enough to be able to perform these operations by hand on reasonably small red-black trees;
• to ensure that you understand the structure and objectives of algorithms on red-black trees well enough to be able to complete (or at least, add more detail to) the proofs of correctness and efficiency of these algorithms that were sketched in class, and
• to ensure that you could use a red-black tree to develop a class that implements either of Java’s Set or Map interfaces.

Students should read through and try to solve the problems on this exercise before attending the tutorial.

Expected Background

This exercise is based on material presented during the lectures on red-black trees. It is expected that students have attended these lectures and carefully reviewed the notes for these classes that are available online.

Red-black trees are also discussed in Chapter 13 of the textbook, Cormen, Leiserson, Rivest and Stein’s, Introduction to Algorithms There is also a very readable Wikipedia article on red-black trees that you might find to be helpful.

Warmup Exercises — To Check That You Understand the Basics

It is to be expected that all of the questions in this first section can be answered by any student who has successfully completed the prerequisites for this course, attended the lectures in which red-black trees were discussed, and read through the material that is listed above.

Teaching assistants will not be spending very much time in tutorials discussing these questions! Students should look at them anyway to make sure that they know how to answer them.

Students who do have difficulty with these questions, after completing the suggested reading, should contact the course instructor to get extra help.

1. Say whether each of the following is a red-black tree, and say why it is (or why it is not one) in each case.

   1. First Tree:

      

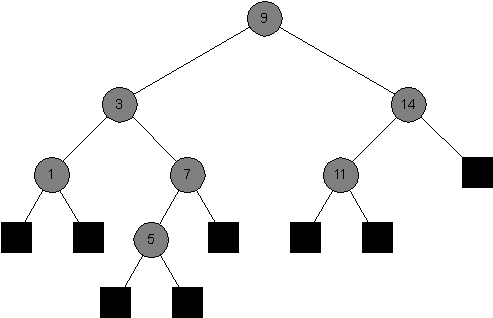
   2. Second Tree:

      

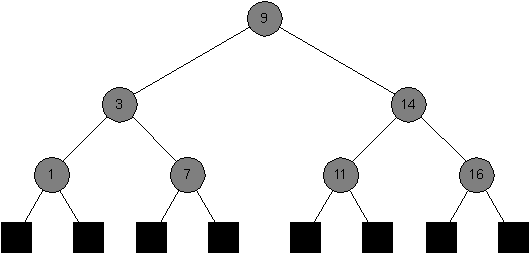
   3. Third Tree:

      

   
   

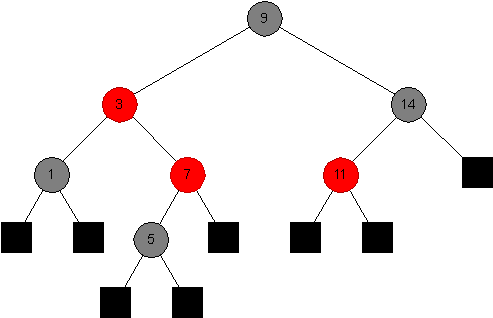
2. Consider the process of inserting a value into a red-black tree.

   1. Draw the tree that would result after inserting an element with key 17 into the following red-black tree.

      

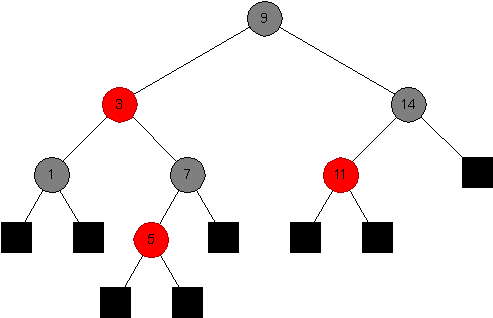
   2. Draw the tree that would result after inserting an element with key 4 into the above tree.

   3. Draw the trees that would result after inserting the following sequence of elements (one after another) into a red-black tree that initially consists of a single leaf.

      1, 2, 3, 4, 5, 6, 7

3. Consider the following red-black tree:

   

   Draw the red-black trees that would result by deleting the following sequence of values (one after another) from this tree:

   9, 1, 3, 7, 11

4. Suppose that a red-black tree was used as the data structure for a class that implements Java’s Set interface.

   1. Which method(s) that are provided by this interface would be implemented by searching in the tree?

   2. Which method(s) that are provided by this interface would be implemented by adding one ore more nodes to the tree?

   3. Which method(s) that are provided by this interface would be implemented by deleting one or more nodes from the tree?

To Be Discussed in the Tutorial

5. During the lectures on red-black trees it was proved that for every node x in a red-black tree, the subtree with root x includes at least

   2^bh(x) − 1

   nodes.

   1. Modify the proof in the notes in order to show that for each node x, the subtree with root x includes at least 2^bh(x)−1 internal nodes, as well.

   2. Now modify the statements and proofs that appear later in the above notes, to prove a useful relationship between the depth of a red-black tree and the size of the sorted set or map that it represents.

   3. After looking at examples of red-black trees, find and write down a relationship between the number of internal nodes and the number of leaves in any red-black tree. (A simple relationship does exist.)

      Try to use mathematical induction to prove the relationship you (seem to have) found.

      What does this tell you about the relationship between the size of the sorted set or mapping represented by a red-black tree T, and the (total) number of nodes in T?

6. Consider a tree that is produced from a red-black tree after a node has been inserted (but the insertion operation has not yet completed). One case that might arise is that a subtree has the following shape.

   

   
   

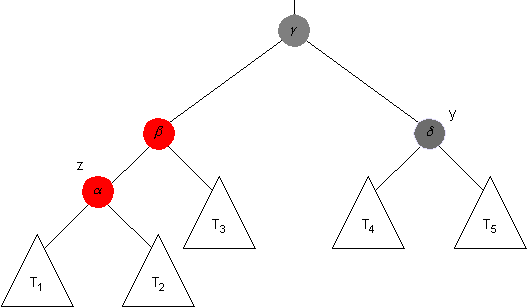
   It is possible that the node with label δ is a leaf (so that T₄ and T₅ are empty trees).

   Recall that the following loop invariant is assumed to hold at this point of the computation: Exactly one of the following conditions is satisfied.

   1. The parent of z is also red.
      All other red-black properties are satisfied.

   2. z is the root.
      All other red-black properties are satisfied.

   3. All red-black properties are satisfied.
      Thus this is a red-black tree.

   Indeed, it is clear from the picture that the first of these conditions is satisfied (if any are) in this particular case. Now consider the following questions.

   1. List all the relationships involving the black-heights of α, β, γ, δ, and the roots of T₁, T₂, T₃, T₄ and T₅ (if the last two trees are nonempty) that must hold, if the loop invariant is satisfied at this point.

   2. Recall that the above subtree is replaced by the following one after the next adjustment is made.

      

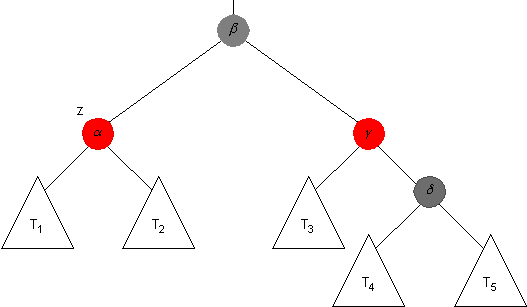
      Explain why the black-heights of each of the nodes in subtrees T₁, T₂, T₃, T₄ and T₅ are well-defined after this adjustment, if the loop invariant was satisfied before it. (This part of the question should be easy!)

   3. Prove that the black-heights of each of α, β, γ, and δ are well-defined after the adjustment, if the loop invariant was satisfied before it.

   4. Prove that the black-height of each ancestor of β is well-defined in the tree after the adjustment, if the loop-invariant was satisfied before it.

   5. Using the above, prove that the loop-invariant is satisfied once again, after the adjustment, if it was satisfied before it.

      If you do not have time to answer this question then you should make sure that, at least, you can list all the properties that you would need to prove in order to answer it.

Additional Problems

Students should also be able to solve the following (similar) problems after participating in the tutorial, but it is not likely that there will be time for them to be discussed in it. Please contact the course instructor if you have tried to answer these questions and would like to get help with them or discuss your answers.

7. The above question asked you to consider the case that was listed as “Case 2” in the lecture notes on rotations and insertions in red-black trees. Answer the above question for each of the other cases (Subcase 1a, subcase 1b, case 3, and the corresponding cases in which the parent of z is a right child) as well.

8. Use the above notes to write pseudocode (possibly including pictures) for the entire insertion algorithm. Use the above information, and fill in any additional details that are needed, to establish the partial correctness of this algorithm.

9. Use the above information, and the information in the above notes, to prove termination as well. Give an upper bound for the number of steps used by this algorithm that depends on either the size or the depth of the input tree.

10. Using Questions 6–9 to figure out how to proceed, fill in the details needed to complete an algorithm for deletion from a red-black tree, along with a proof of its correctness and efficiency.

    If you do not have time for all of this then, at least, you try to consider “Case 3a” (from the notes on deletion) in detail — following a process that is similar to the one you followed in Question 4, above.

11. If you have checked the other references for red-black trees that are listed above then you have probably noticed that the descriptions of red-black trees and their algorithms are not, quite, the same in any two of these references!

    1. Confirm that — apart from reasonably minor implementation details — each reference really is describing the same data structure.

    2. Compare the different algorithms for insertion into red-black trees that are described. Do you think that the algorithms really are different, or is the same algorithm just being described in different ways? (In particular, would different trees be generated when the same keys are inserted into an empty tree, using each of these algorithms?)

    3. Compare the different algorithms for deletion from red-black trees. Are these algorithms different, or is the same algorithm being described in different ways?

---

Last updated: http://www.cpsc.ucalgary.ca/~jacobs/Courses/cpsc331/W17/tutorials/tutorial15.html