Tutorial 19, CPSC 331, Winter 2017

Tutorial 1 -  Tutorial 2 -  Tutorial 3 -  Tutorial 4 -  Tutorial 5 -  Tutorial 6 -  Tutorial 7 -  Tutorial 8 -  Tutorial 9 -  Tutorial 10 -  Tutorial 11 -  Tutorial 12 -  Tutorial 13 -  Tutorial 14 -  Tutorial 15 -  Tutorial 16 -  Tutorial 17 -  Tutorial 18 -  Tutorial 19 -  Tutorial 20 -  Tutorial 21 -  Tutorial 22 -  Tutorial 23 -  Tutorial 24

Binary Heaps and Their Applications

About This Exercise

The objectives of this exercise

• to ensure that you understand the structure of a binary heap and its implementation using an array

• to ensure that you understand operations on binary heaps well enough to be able to describe their overall structure, give pseudocode for them, and trace their execution by hand on small examples

• to ensure that you understand the HeapSort algorithm well enough to describe it (using operations on binary heaps), trace its execution by hand on small examples, and state its worst-case running time

• to ensure that you are familiar with the priority queue abstract data type, understand its importance, how it can be implemented using a binary heap, and how this is supported in Java.

Students should read through and try to solve the problems on this exercise before attending the tutorial.

Expected Background

This is based on material provided in lectures that introduce binary heaps, present algorithms for operations on binary heaps, and present their applications.

Warmup Problems — To Check That You Understand the Basics

It is to be expected that all of the questions in this first section can be answered by any student who has successfully completed the prerequisites for this course, and attended the lectures in which binary heaps were discussed (reviewing the online notes, as needed).

These warmup problems will not be discussed in the tutorial; students who do have difficulty with them should contact the course instructor to get extra help.

1. Describe each of the following properties of a binary heap.

   1. Describe the shape of a binary heap with size n for any nonnegative integer n.
   2. Describe the relationship between the size and the depth of any heap.
   3. Describe how the elements of a max-heap must be ordered.
   4. Describe how the elements of a min-heap must be ordered.
   5. Describe how the entries of a heap can be stored in an array. If the contents of a node are stored at index i, then where are the contents of this node’s parent, left child, and right child stored?

2. Give an array of length 10 that represents the following heap.

   

    

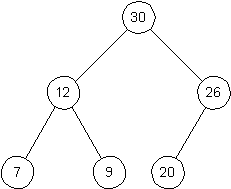
3. Draw the heap that is represented by the following array A, assuming that heap-size(A)=6.

   

    

4. Use English or pseudocode to describe algorithms to do each of the following.

   1. insert a value into a Max-Heap
   2. remove the largest value from a Max-Heap

   State the number of operations used by each operation in the worst case, as a function of the size of the heap. You may use asymptotic notation to give your answer.

5. Use English or pseudocode to describe the HeapSort algorithm, using algorithms to solve the problems mentioned in the previous question as subroutines. Then trace the execution of this algorithm to sort the following array.

   

    

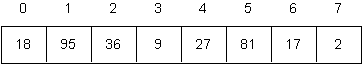
6. At this point in the course you know about two different sorting algorithms that use Θ(n log n) time to sort an array of length n in the worst case — MergeSort and HeapSort. It was suggested in class that, due to its simplicity, MergeSort might be faster (perhaps by a small constant factor) and might be easier to implement.

   Describe an advantage that HeapSort has over MergeSort.

7. Define a priority queue, say what operations it supports, and explain how a priority queue can be implemented using a binary heap.

8. Consider the PriorityQueue<E> class that is currently provided as part of Java Collections framework.

   Compare (and contrast) the methods provided by this Java class to the operations on priority queues that were described in class. How would you implement the kind of “priority queue” described in class using Java’s PriorityQueue class?

To Be Discussed in the Tutorial

9. In this question you will show that it is possible to perform the first half of the HeapSort algorithm much more quickly — an arbitrary array (of elements of some ordered type) can be turned into a Max-Heap using time that is only linear in the length of the array.

   1. Consider a “Heapify” operation on an array, that takes an index i (greater than or equal to 0 and less than the length of the array) as input, and that rerranges the elements of the subtree with root at position i, in the binary tree represented by this array, so that this subtree has Max-Heap order. The elements of the array that are not in this subtree should not be moved.

      For example, if an array (and the binary tree) is as follows,

      
      

      

      
      

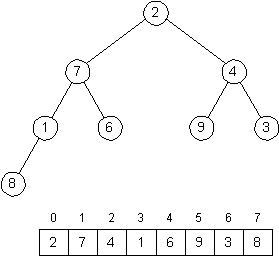
      and heapify(1) is performed using this array, then the resulting array (and binary tree) should be produced.

      
      

      

      
      

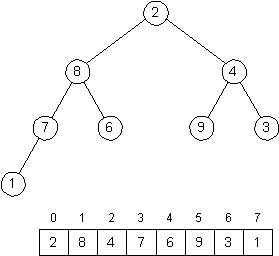
      Consider a recursive implementation of this, so that we start to perform the operation heapify(i) by performing the operations heapify(i.left) and heapify(i.right).

      For example, we would begin to carry out the operation heapify(0) by performing the operations heapify(1) and heapify(2), which would result in the following array (and binary tree).

      
      

      

      
      

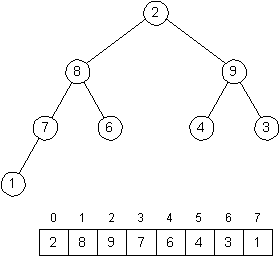
      Describe how you could finish this — in this case, turning the entire structure that looks the the following heap,

      
      

      

      
      

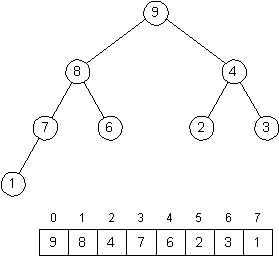
      using a number of steps that is at most logarithmic in the size of the subtree with root i.

   2. Using the above, give (reasonably complete) pseudocode for the heapify operation that has now been informally described.

   3. Let T(m) be the number of steps used by this method in the worst case, where m is the size of the subtree whose root is the input for heapify. Let m_L and m_R the the sizes of the left and right subtrees of this subtree.

      Using the above information, show that if m ≥ 2 then T(m) satisfies the following inequality:

      T(m) ≤ T(m_L) + T(m_R) + c log m

      for some positive constant c.

   4. Use the above to prove that T(m) ∈ O(m).

      Hint: It will be helpful to try to show that, for sufficiently large m,

      T(m) ≤ c₁ m − c₂ log m

      for positive constants c₁ and c₂. The fact that the second term is being subtracted away will actually make the proof easier, here!

   5. Now, use the above to describe another, faster, version of HeapSort. This will still use cn log n steps to sort an array of length n in the worst case, for sufficiently large n and a positive constant c, but the value of the multiplicative constant c will be reduced.

   6. Finally, show that the new algorithm still uses Ω(n log n) steps in the worst case — while the new algorithm really is faster (when its input is large) its cost has not been improved by more than a constant factor.

---

Last updated: http://www.cpsc.ucalgary.ca/~jacobs/Courses/cpsc331/W17/tutorials/tutorial19.html