
Digital Earth Workshop, September 13-14, 2014
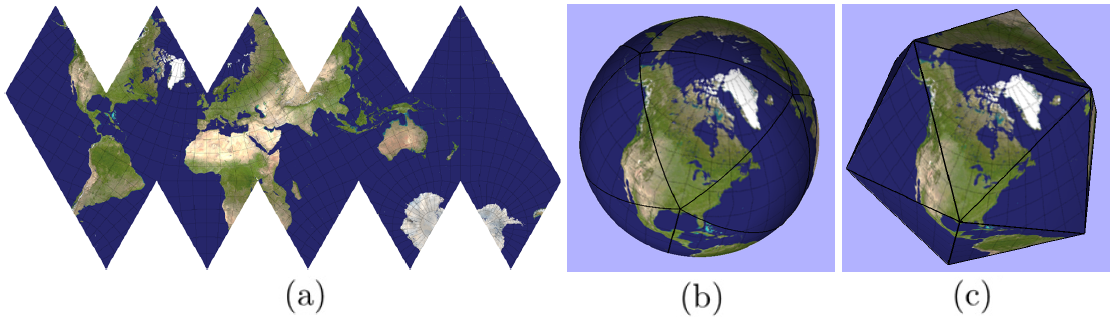
The digital Earth framework is a multiresolution 3D model used to visualize location-based data. In [1], we introduce a new digital Earth framework using a cube as its underlying polyhedron. To create multiresolution, we introduce two types of 1-to-2 refinement. Having a smaller factor of refinement enables us to provide more resolutions and therefore a smoother transition among resolutions. We also suggest two indexing methods specifically designed for quadrilateral cells resulting from 1-to-2 refinement. We finally discuss the equal area spherical projection that we are using in this framework to model the Earth as a sphere partitioned to equal area cells. See [1] for more details.
Modern area preserving projections employed by cartographers and geographers have closed forms when transitioning between the sphere and the plane. Inversions - from the planar map to the spherical approximation of the Earth - are slower, requiring iterative root finding approaches or entirely undetermined. Recent optimizations of the common Inverse Snyder Equal Area Polyhedral projection have been fairly successful, however the work herein improves it further by adjusting the approximating polynomial. An evaluation against the original and improved optimizations is provided, along with a previously unexplored real-time analysis. See [2] for further details.
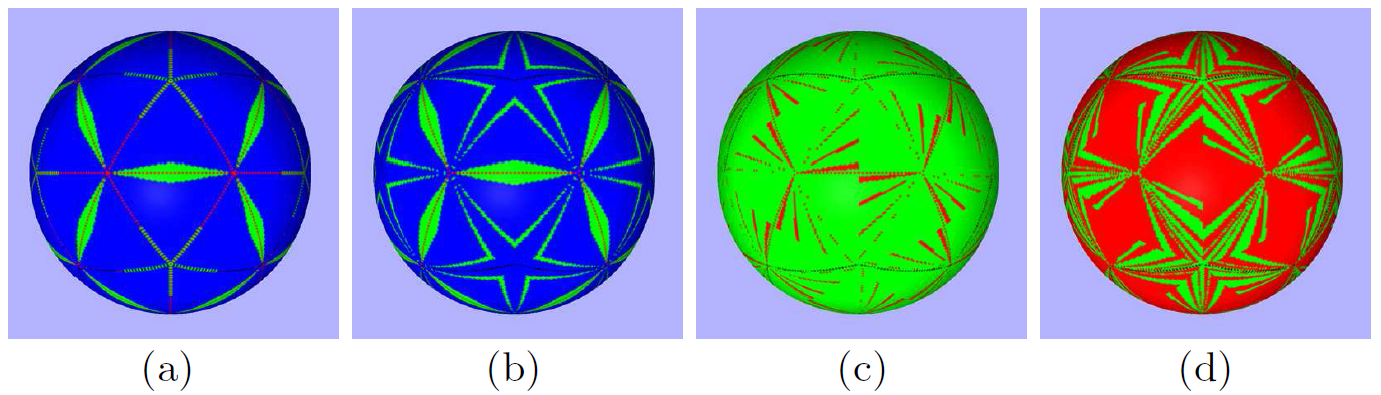
Modern techniques in area preserving projections used by cartographers and other geospatial researchers have closed forms when projecting from the sphere to the plane, as based on their initial derivations. Inversions, from the planar map to the spherical approximation of the Earth which are important for modern 3D analysis and visualizations, are slower, requiring iterative root finding approaches, or not determined at all. We introduce optimization techniques for Snyder’s inverse polyhedral projection by reducing iterations, and using polynomial approximations for avoiding them entirely. Results including speed up, iteration reduction, and error analysis are provided. For additional details, see [3].
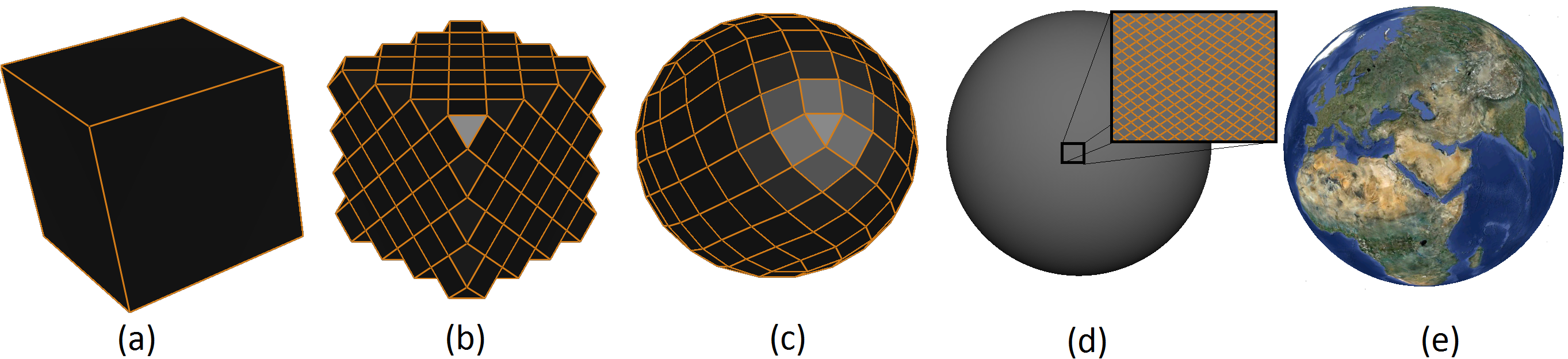
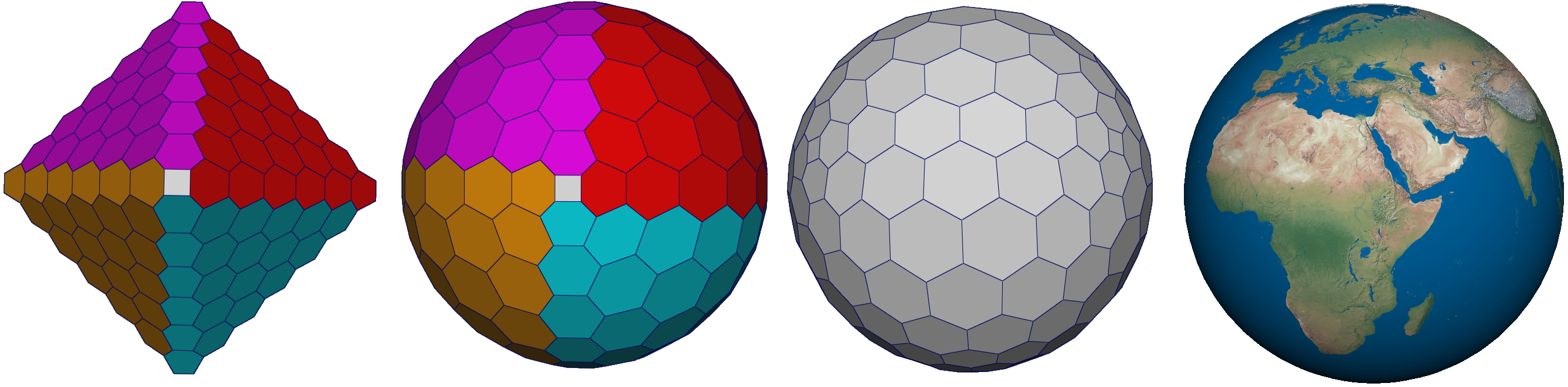
Geospatial data is gathered through a variety of different methods. The integration and handling of such data-sets within a Digital Earth framework are very important in many aspects of science and engineering. One means of addressing these tasks is to use a Geodesic Discrete Global Grid System and map points of the Earth’s surface to cells. An indexing mechanism is needed to access the data and handle data queries within these cells.. In [4], we present a general hierarchical indexing mechanism for hexagonal cells resulting from the refinement of triangular spherical polyhedra representing the Earth. In this work, we establish a 2D hexagonal coordinate system and diamond-based hierarchies for hexagonal cells that enables efficient determination of hierarchical relationships for various hexagonal refinements, and demonstrate its usefulness in Digital Earth frameworks. See [4] for more details.
Digital Earth frameworks provide a tool to receive, send and interact with large location-based data sets, organized usually according to Discrete Global Grid Systems (DGGS). In DGGS, an indexing method is used to assign a unique index to each cell of a global grid and the data sets corresponding to these cells are retrieved or allocated using this unique index. There exist many methods to index cells of DGGS. Toward facility, interoperability, and also defining a “standard” for DGGS, a conversion is needed to translate a data set from one DGGS to another. In [5], we first propose a categorization of indexing methods of DGGS and then define a general conversion method from one indexing to another. Several examples are presented to describe the method. See [5] for more details.

With the help of the development team in PYXIS Inc., our research has been integrated in Worldview ( https://www.worldview.gallery/PYXIS ) (see the below figure). In PYXIS worldview, data sets from different resources and different formats can be integrated together for the purpose of data analysis, visualization, etc. Currently, PYXIS worldview is successfully used in educational environments and we hope that we can release a version for the public use in the near future. Having, such a goal in mind, many new research areas needed to be investigated such as data transmission, compression, etc.

Related Papers
[1] One-to-two digital earth, Ali Mahdavi-Amiri, Faraz Bhojani, and Faramarz Samavati, Advances in Visual Computing - ISVC 2013, LNCS 8034, Springer Berlin Heidelberg, pp. 681-692 (Jul 2013) ![]()
![]()
![]()
[2] Analysis of inverse Snyder optimizations, Erika Harrison, Ali Mahdavi-Amiri, and Faramarz Samavati, Transactions on Computational Science XVI, LNCS 7380, Springer Berlin Heidelberg, pp. 134-148 (2012) ![]()
![]()
![]()
[3] Optimization of inverse Snyder polyhedral projection, Erika Harrison, Ali Mahdavi-Amiri, and Faramarz Samavati, International Conference on Cyberworlds (CW), in association with ACM SIGGRAPH and Eurographics, IEEE Computer Society, pp. 136-143 (Oct 2011) ![]()
![]()
![]()
[4] Hexagonal Connectivity Maps for Digital Earth, Ali Mahdavi-Amiri, Erika Harrison, Faramarz Samavati International Journal of Digital Earth, (2014) ![]()
![]()
![]() ?
?
[5] Categorization and Conversions for Indexing Methods of Discrete Global Grid Systems, Ali Mahdavi-Amiri, Faramarz Samavati, Perry Peterson, ISPRS International Journal of Geo-Information, (2015) ![]()
![]()
![]() ?
?
PhD Thesis
[1] ACM: Atlas of Connectivity Maps, Ali Mahdavi-Amiri, 2015 ![]()
