Tutorial 10, CPSC 331, Fall 2008

Algorithms for Searching

About This Exercise

This exercise is based on material presented during the lecture on October 29.

The objectives of this exercise are

to ensure that you understand the definitions of the searching problems that were discussed;
to ensure that you understand the algorithms for searching included in these lectures. You should be able to
- trace the execution of these algorithms by hand on small examples,
- explain what these algorithms do, both by giving simple English descriptions and providing pseudocode for them,
- understand the proofs of correctness and efficiency of these algorithms, and
- understand and be able to apply the results that were presented about the worst-case running times of these algorithms;
to ensure that you could implement these algorithms by writing Java programs for them (and, ideally, writing programs using other programming languages as well).

Please read through and try to solve the problems on this exercise before attending the tutorials on November 3-5. Problems on this exercise will be discussed during this tutorial.

Note that some of these questions ask you to verify statements that were made by the instructor in class when these algorithms were presented. Students who did not attend the lectures on this topic might find it helpful to ask students who were present in class about what was said about the correctness of these algorithms in class before they spend time on this exercise.

Problems

Consider the following array A.

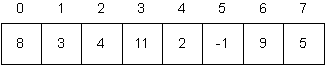
Trace the execution of the “Linear Search” algorithm when it is used to search for each of 2, 5, and 7 in this array.
Consider the following sorted array A.
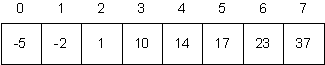
1. Trace of the execution of the “Linear Search” algorithm for the original Searching Problem, when it is used to search for each of 1, 37, −6, 12, and 38 in this array. That is, show what happens if you search for these values and you do not know that (or take advantage of the fact that) this is a sorted array.
2. Repeat the above question, using the “Linear Search” algorithm for a sorted array, instead.
3. Repeat the above question, using the “Binary Search” algorithm instead.
Consider the problem of “Searching in a Sorted Array,” and the version of the “Linear Search” algorithm that is given for this problem (this is the second of the three algorithms presented in the lecture notes).

Let I[ j ] be the “loop invariant” that is given for the loop in this algorithm.
1. After an inspection of the code, explain why the conditions in I[0] are all satisfied just before for the first execution of the loop body.
2. Let j be a nonnegative integer such that the loop body is executed at least j times.
  
  Suppose the loop invariant I[ j ] is satisfied just after the j^th execution of the loop body. Show that if the loop test succeeds, and the loop body is executed again, then the conditions in the loop invariant I[j+1] are all satisfied immediately after the j+1^st execution of the loop body, as well.
  
  Verify that this implies that the conditions in I[ j ] are all satisfied immediately after the j^th execution of the loop body (if the loop body is executed j or more times) for every nonnegative integer j.
3. Now suppose that the loop body is executed j times but there is not a j+1^st execution of the loop body — because the condition in the loop test is false after the j^th execution of the loop body.
  
  Use the loop invariant to to argue that if i≥n at this point, then A[h]<k for every integer h such that 0≤h≤n-1.
  
  Then use the loop invariant to argue that if i<n and A[i]≠k, then A[k]>k so that, in fact,
  - A[h]<k for every integer h such that 0≤h<i, and
  - A[h]>k for every integer h such that i≤h≤n-1.
4. Use all the above to establish the “partial correctness” of this linear search algorithm.
5. Finally, show that the function f(n, i) = n−i is a “loop variant” for the loop in this algorithm.
  
  Use this to show that if the algorithm is executed when the precondition is satisfied then it does eventually terminate (so that the algorithm is also “correct”), and that the number of steps used by the algorithm is linear in the size of the input array, in the worst case.
Now consider the behaviour of the “Binary Search” algorithm when it is given a key k to search for and used to search in a sorted array A of size n.

Consider, also, the “Specification of Requirements” for the bsearch subroutine that are given in the lecture notes.
1. Confirm that the precondition for the subroutine is satisfied when the subroutine is called by the main algorithm (with low=0 and high=n−1).
2. Confirm that the precondition implies that k is not an element of the array A if high=low−1. (Why is that?)
3. Confirm that the precondition implies that if low=high then either A[low]=k or k is not an element of the array at all. (Why?)
4. Use the above to argue that if bsearch is called with its precondition satisfied, and with low≥high, then the bsearch produces the output is should: It returns an index h such that A[h]=k if k is an element of the array, and it throws a KeyNotFoundException otherwise.
5. Now consider the more interesting case that low<high. Notice that the subroutine might call itself recursively in this case.
  
  Argue that the subroutine’s precondition is satisfied if it recalls itself recursively. This is not entirely trivial, because the values for “low” and “high” mentioned in the precondition are the first and second inputs supplied to bsearch during this next recursive call (that is, low and mid−1, respectively, in one case, and mid+1 and high, respectively, in another case).
  
  Suppose that the outputs received by this “next” recursive application are correct. After an inspection of the code, confirm that the “current” application of the bsearch subroutine will produce the output that it should, as well.
  
  This can all be used to establish the “partial correctness” of the Binary search algorithm.
Continue to consider the “Binary Search” algorithm the “bsearch” subroutine that does all the work.
1. Suppose the subroutine is called with (the first two) inputs low and high such that
  
  high = low + 2k − 1
  
  so that the part of the array that remains to be searched has size high−low+1=2k.
  
  Show that if bsearch calls itself recursively, then it does to so search a part of the array that has size at most k.
2. Suppose, instead, that bsearch is called with inputs low and high such that
  
  high = low + 2k,
  
  so that the part of the array that remains to be searched has size 2k+1.
  
  Show that if bsearch calls itself recursively, then it does so to search a part of the array that has size at most k in this case, as well.
3. Notice that if bsearch is called when low=high (to search a part of an array with size one) then it calls itself at most once more.
4. Use all of the above to show that if the Binary Search is run on an array of size n, for n≥1, then the total number of calls made to bsearch is at most ⌈log₂n⌉+2.
Use the results of the last two questions to argue that the “Binary Search” algorithm is correct and, furthermore, that it can be used to search in a sorted array of size n using Θ(log₂n) operations in the worst case.
Challenge Question

The “Binary Search” algorithm in the lecture notes is somewhat wasteful: It compares A[mid] to k in two ways (in the worst case).

Consider a version of the algorithm in which you do not perform the second of these tests: Rather than choosing between the output of bsearch(mid+1, high, k) and the value mid, this version of the algorithm returns the output of bsearch(mid, high, k).
1. What additional changes (if any) do you need to make to produce another algorithm that is also correct?
  
  Consider the three cases high=low−1, high=low, and high=low+1 carefully!
2. After making an additional changes that are needed, give pseudocode for a version of the bsearch algorithm that uses fewer comparisons in the worst case.
3. Then modify the claims that were given for the original algorithm to produce similar claims that are satisfied by your version of the algorithm instead. Use these to prove that your algorithm is correct and efficient.
Write Java programs that implement the given search algorithms. Try to make your implementation as general possible — in particular, make as few assumptions about the types of values being stored in the array as possible.
Which, if any, of the search algorithms could be modified to search efficiently in a linked list whose elements are in sorted order?

This page last modified:
http://www.cpsc.ucalgary.ca/~jacobs/cpsc331/F08/tutorials/tutorial10.html