Tutorial 14, CPSC 331, Fall 2008

home page -  news -  syllabus -  schedule -  assignments -  tutorials -  tests -  java -  references -  Mike Jacobson

Tutorial 1 -  Tutorial 2 -  Tutorial 3 -  Tutorial 4 -  Tutorial 5 -  Tutorial 6 -  Tutorial 7 -  Tutorial 8 -  Tutorial 9 -  Tutorial 10 -  Tutorial 11 -  Tutorial 12 -  Tutorial 13 -  Tutorial 14 -  Tutorial 15 -  Tutorial 16

 Graphs and their Representations

About This Exercise

This exercise is based on the information on graphs and their representations that was presented during lectures on November 21.

The objectives of this exercise are

Please read through and try to solve the problems on this exercise before attending the tutorials on November 26.

Problems

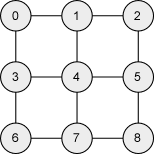
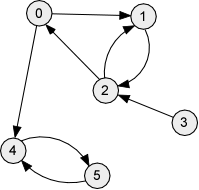
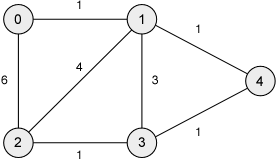
  1. Draw adjacency-matrix and adjacency-list representations for each of the following graphs.

    1.  

      An Undirected Graph

    2.  

      A Directed Graph

    3.  

      A Weighted Graph

  2. Write a Java program that could be used to convert an adjacency-matrix representation of a graph into an adjacency-list representation of the same graph.

  3. Describe how to modify each of the adjacency-matrix and adjacency-list representatives, in order to allow new vertices to be added more efficiently.

    Try to produce representations that resemble the ones that have been described but also have behaviour similar to array-based representations of stacks and queues: While the occasional operation might be expensive the total cost of a collection of operations (that add new vertices) should be linear in the number of operations considered.

  4. An undirected graph G=(V, E) is connected if there is a path between every pair of vertices u and v in G.

    The goal of this question is to prove the following: Every connected graph with n vertices must have at least n−1 edges.

    1. Show that if a graph has two or more vertices and it does not have any edges at all then this graph is not connected.

    2. Now let G=(V, E) be an arbitrary graph such that V includes n vertices and E includes at most n−2 edges.

      Prove that G cannot be a connected graph, in this case, if either n=1 or n=2.

    3. Another easy case is as follows: Show that if n≥2 and G includes at one or more vertices whose degree is zero, then G is not a connected graph.

    4. To continue, recall that the sum of the degrees of the nodes in an undirected graph is always equal to two times the number of edges (since each edge is incident on exactly two vertices).

      Use this relationship to prove that if G is an undirected graph with n ≥ 3 vertices and at most n−2 edges, then G must have at least one vertex v whose degree is at most one.

      If the degree of v is zero then above easy case applies. Otherwise a smaller undirected graph (that has n−1 vertices and at most n−3 edges) can be obtained by removing v along with the edge on which it is incident.

      Show that this smaller undirected graph is connected if and only if G is.

    5. Use all of the above to show that if G is an undirected graph with n vertices and strictly fewer than n−1 edges then G is not a connected graph. Note that this is equivalent to the property that was given at the beginning of this question.

This page last modified:
http://www.cpsc.ucalgary.ca/~jacobs/cpsc331/F08/tutorials/tutorial14.html