Tutorial 8, CPSC 331, Fall 2008

Red-Black Trees

About This Exercise

This exercise is based on material presented during the lectures on Wednesday, October 8, Friday, October 10, and Friday, October 17.

The objectives of this exercise are

to ensure that you understand the definition and basic properties of a red-black tree,
to ensure that you understand operations on red-black trees well enough to be able to perform these operations by hand on reasonably small red-black trees,
to ensure that you understand the structure and objectives of algorithms on red-black trees well enough to be able to complete (or, at least, add more detail to) the proofs of correctness of these algorithms that were sketched in class, and
to ensure that you can use a red-black tree to develop a class that implements a “SortedSet” or “SortedMap” interface in Java.

Please read through and try to solve the problems on this exercise before attending the tutorials during October 20 to 24.

Problems

Say whether each of the following is a red-black tree, and say why it is (or why it is not one) in each case.
1. First Tree:
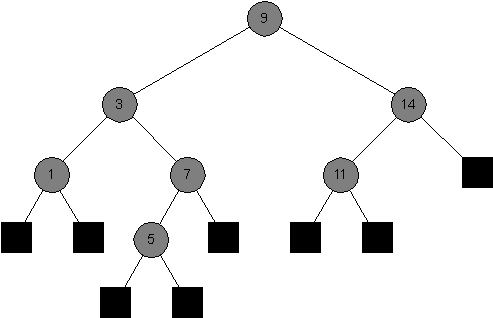
2. Second Tree:
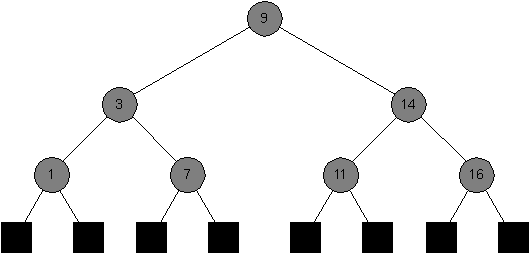
3. Third Tree:
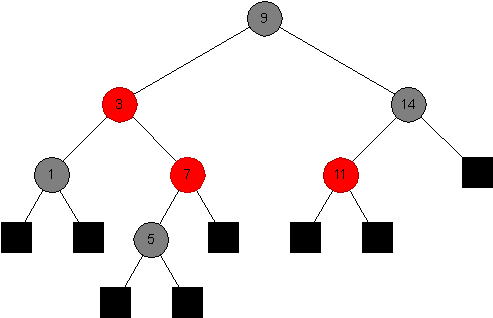
Consider the process of inserting a value into a red-black tree.
1. Draw the tree that would result after inserting an element with key 16 into the following red-black tree.
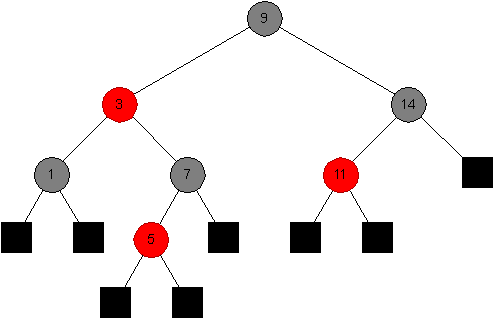
2. Draw the tree that would result after inserting an element with key 4 into the above tree.
3. Draw the trees that would result after inserting the following sequence of elements (one after another) into a red-black tree that initially consists of a single leaf.
  
  1, 2, 3, 4, 5, 6, 7
Consider the following red-black tree:

Draw the red-black trees that would result by deleting the following sequence of values (one after another) from this tree:

9, 1, 3, 7, 11
During the first lecture on red-black trees it was proved that for every node x in a red-black tree, the subtree with root x includes at least

2^bh(x) − 1

nodes.
1. Modify the proof in the notes in order to show that for each node x, the subtree with root x includes at least 2^bh(x)−1 internal nodes, as well.
2. Now modify the statements and proofs that appear later in the above notes, to prove a useful relationship between the height of a red-black tree and the size of the sorted set or mapping that it represents.
3. After looking at examples of red-black trees, find and write down a relationship between the number of internal nodes and the number of leaves in any red-black tree. (A simple relationship does exist.)
  
  Try to use mathematical induction to prove the relationship you (seem to have) found.
  
  What does this tell you about the relationship between the size of the sorted set or mapping represented by a red-black tree T, and the (total) number of nodes in T?
Consider a tree that is produced from a red-black tree after a node has been inserted (but the insertion operation has not yet completed). One case that might arise is that a subtree has the following shape.

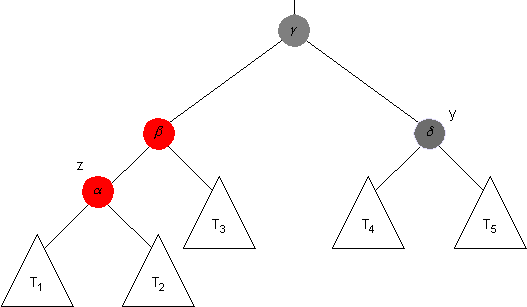
It is possible that the node with label δ is a leaf (so that T₄ and T₅ are empty trees).

Recall that the following loop invariant is assumed to hold at this point of the computation: Exactly one of the following conditions is satisfied.
1. The parent of z is also red.
  All other red-black properties are satisfied.
2. z is the root.
  All other red-black properties are satisfied.
3. All red-black properties are satisfied.
  Thus this is a red-black tree.
Indeed, it is clear from the picture that the first of these conditions is satisfied (if any are) in this particular case. Now consider the following questions.
1. List all the relationships involving the black-heights of α, β, γ, δ, and the roots of T₁, T₂, T₃, T₄ and T₅ (if the last two trees are nonempty) that must hold, if the loop invariant is satisfied at this point.
2. Recall that the above subtree is replaced by the following one after the next adjustment is made.
  
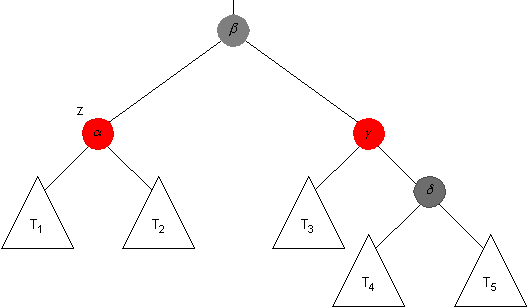
  Explain why the black-heights of each of the nodes in subtrees T₁, T₂, T₃, T₄ and T₅ are well-defined after this adjustment, if the loop invariant was satisfied before it. (This part of the question should be easy!)
3. Prove that the black-heights of each of α, β, γ, and δ are well-defined after the adjustment, if the loop invariant was satisfied before it.
4. Prove that the black-height of each ancestor of β is well-defined in the tree after the adjustment, if the loop-invariant was satisfied before it.
5. Explain why the black-heights of every other node in the tree is well-defined after the adjustment, if the loop invariant was satisfied before it.
6. Using the above, prove that the loop-invariant is satisfied once again, after the adjustment, if it was satisfied before it.
  
  If you do not have time to answer this question then you should make sure that, at least, you can list all the properties that you would need to prove in order to answer it.
The above question asked you to consider the case that was listed as “Case 3” in the lecture notes on rotations and insertions in red-black trees.

Answer the above question for each of the other cases (Subcase 1a, subcase 1b, case 3, and the corresponding cases in which the parent of z is a right child) as well.
Use the above notes to write pseudocode (possibly including pictures) for the entire insertion algorithm. Use the above information, and fill in any additional details that are needed, to establish the partial correctness of this algorithm.
Use the above information, and the information in the above notes, to prove termination as well. Give an upper bound for the number of steps used by this algorithm that depends on either the size or the height of the input tree.
Using Questions 5–8 to figure out how to proceed, fill in the details needed to complete an algorithm for deletion from a red-black tree, along with a proof of its correctness and efficiency.

If you do not have time for all of this then, at least, you try to consider “Case 3a” (from the notes on deletion) in detail — following a process that is similar to the one you followed in Question 4, above.
Write Java programs to do each of the following.
1. Search for a given element in a given red-black tree.
2. Insert a given value into a given red-black tree.
3. Delete a given value from a given red-black tree.

This page last modified:
http://www.cpsc.ucalgary.ca/~jacobs/cpsc331/F08/tutorials/tutorial8.html