| Heaps and Heap Sort |
About This Exercise
This exercise is based on the information on binary heaps, operations on binary heaps, heap sort, and priority queues that was presented during lectures on November 5–14.
The objectives of this exercise are
- to ensure that you understand the structure of a binary heap and its implementation using an array,
- to ensure that you understand the Heap Sort algorithm and its analysis, and
- to ensure that you understand the implementation of a priority queue using a binary heap, including the algorithms used to support this abstract data type’s operations.
Please read through and try to solve the problems on this exercises before attending the tutorials on November 17. These problems will be discussed during these tutorial.
Problems
-
Give an array of length 10 that represents the following heap.
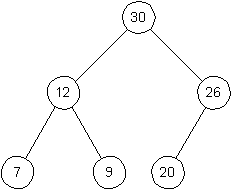
-
Draw the heap that is represented by the following array A, assuming that heap-size(A)=6.

-
Suppose A is the array you produced when you answered Question 1.
Draw the heap, and its array representation, that you could obtain by performing each of the following operations.
- Delete-Min(A)
- Increase-Key(A, 3, 14)
- Insert(A, 28)
-
Repeat the previous question, using the heap A that was given for Question #2 (assuming again that heap-size(A)=6).
-
Use Heap Sort to sort the following array. Draw the binary trees that correspond the array as Build-Max-Heap is applied at the beginning of this operation, as well as the heaps and arrays that are generated using Delete-Max after that.
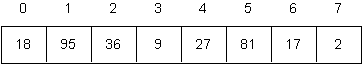
-
Write a Java program that implements the Heap Sort algorithm to sort a given array. Try to make your program as general as you can.
-
Consider the following algorithm. Its inputs are an array A that represents a nonempty binary tree with the shape of a heap, and an integer i such that 0 ≤ i < heap-size(A). Its output should be the largest element stored in the subtree of A with root i.
Find-Maximum(A, i) largest = A[i] if left(i) < heap-size(A) then largest = max(largest, Find-Maximum(A, left(i))) end if if right(i) < heap-size(A) then largest = max(largest, Find-Maximum(A, right(i))) end if
- Sketch a proof that this algorithm is correct.
- Sketch a proof that the number of steps is linear in the size of the subtree whose root is the value stored at A[i] in the worst case.
-
This question, and the question that follows, concerns two different recursive algorithms that can be used to rearrange the elements of a binary tree (with the same shape as a heap) in order to produce a max-heap.
-
Modify the above “Find-Maxiumum” procedure so that it also returns the index j in A of the largest value that it found. The new algorithm not be significantly more expensive than the algorithm given above.
-
Consider a recursive algorithm “Build-Max-Heap2” that receives the same inputs as the above algorithm “Find-Maximum.” This recursive algorithms should rearrange the values stored in the subtree with root A[i] in order to produce a max-heap.
The algorithm includes the following three steps.
-
Use the algorithm described in the first part of the question to find the largest value stored in the subtree with root A[i] along with its index j. Swap the values stored at indices i and j, so the largest values in the subtree is stored at the root.
-
if left(i) < heap-size(A) then apply the Build-Max-Heap2 algorithm recursively to convert the left subtree into a max-heap.
-
if right(i) < heap-size(A) then apply the Build-Max-Heap2 algorithm recursively to convert the right subtree into a max-heap.
Sketch a proof that this recursive algorithm is correct. Then state a bound on the worst-case running time of this algorithm and prove that your bound is correct.
-
-
-
Finally, consider yet another recursive algorithm, “Build-Max-Heap3,” which should solve the same problem as Build-Max-Heap2. This algorithm should use the following steps.
-
if left(i) < heap-size(A) then apply the Build-Max-Heap3 algorithm recursively to convert the left subtree into a max-heap.
-
if right(i) < heap-size(A) then apply the Build-Max-Heap3 algorithm recursively to convert the right subtree into a max-heap.
-
Apply the Max-Heapify algorithm (discussed in class) with inputs A and i.
Sketch a proof that this recursive algorithm is also correct. Then state a bound on the worst-case running time of this algorithm and prove that your bound is correct.
-
Note: One of the recursive algorithms “Build-Max-Heap2” and “Build-Max-Heap3” is asymptotically as efficient as the “Build-Max-Heap” algorithm discussed in class, but the other is not.
You should be able to analyze both recursive algorithms (and discover which is better for large inputs) by studying and modifying the analyses that are included in the lecture notes on heap operations and heap sort.
|
This page last modified:
http://www.cpsc.ucalgary.ca/~jacobs/cpsc331/F08/tutorials/tutorial12.html |