| Quicksort |
About This Exercise
This exercise is based on the information on Quicksort that was presented during lectures on November 17.
The objectives of this exercise are
- to ensure that you can trace the execution of the Quicksort by hand on small examples,
- to ensure that you can implement the Quicksort algorithm as a Java program,
- to ensure that you understand the Quicksort algorithm, as well as its analysis, well enough to be able to modify these.
Please read through and try to solve the problems on this exercise before attending the tutorials on November 19. Problems on this exercise will be discussed in these tutorials.
Problems
-
Consider the following array.
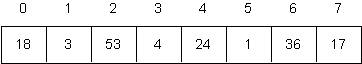
-
Trace the execution of the “Deterministic Partitioning” algorithm on this input. That is, trace the execution of the program after the call
DPartition(A, 0, 7)
if A is the array that is shown above.
-
Notice that this is the first stage of the application of the deterministic “Quicksort” algorithm to sort the above array.
Trace the rest of the application of this algorithm to sort this array. In order to answer this question you should list each of the following.
- the calls that are made to DPartition after this
- the array before each of these calls is made
- the array after each of these calls is completed
-
-
Repeat the above question, using the following array instead of the one that is shown above.
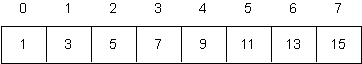
-
Repeat the first question, using the following array instead of the ones that are shown above.
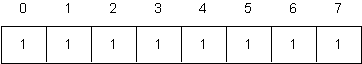
-
Consider the application of the randomized Quicksort algorithm to sort the above arrays instead of the deterministic algorithm. In each case, compare this to the performance of the randomized algorithm to the performance of the deterministic algorithm on the given input, and say whether you would expect the performance of the randomized algorithm to be
- better than that of the deterministic algorithm,
- worse than that of the deterministic algorithm, or
- approximately the same as that of the deterministic
algorithm.
-
If you completed the above questions then you should have noticed the following: Neither the deterministic nor the randomized algorithms that have been described in class and in the textbook work particularly well on arrays that include many copies of the same input entry.
-
Modify the “DPartition” algorithm so that it reorders the input algorithm in much the same way as before. However, the algorithm should now move all copies of the pivot element x into the middle of the part of the array that is being processed, and it should return a pair of integers i and j, on inputs A, p, and r, such that the following properties are satisfied.
-
p ≤ i < j ≤ r.
-
For an integer h, if p ≤ h < i then A[h] < x.
-
For an integer h, if i ≤ h ≤ j then A[h] = x.
-
For an integer h, if j < h ≤ r then A[h] > x.
Then modify the proof of correctness and efficiency of the DPartition algorithm to show that your new algorithm is correct and efficient as well.
-
-
Describe a modified version of the deterministic Quicksort algorithm that uses your new partitioning algorithm, and that has better performance when the input array includes many copies of the same algorithm.
-
Make similar modifications to the randomized algorithm. Explain why the resulting algorithm can be expected to perform well on all input arrays.
-
-
Section 8.3 of the textbook describes a different algorithm that can be used to partition. The algorithm partitions a subarray that begins at index p and ends at index r, as before. However, it uses the leftmost value in this subarray as the partition element instead of the rightmost value, and it keeps track of two positions in the array instead of a single one.
The description of the algorithm found in this section of the textbook is extremely helpful, but it is a bit vague. Somewhat more detailed pseudocode for this algorithm is as follows.
x := A[p] right := p+1; left := r while (left ≥ right) do while ((A[right] < x) and (right ≤ r)) do right := right + 1 end while while ((A[left] ≥ x) and (left > p)) do left := left − 1 end while if (left ≥ right) then tmp := A[left]; A[left] := A[right]; A[right] := tmp right := right + 1; left := left − 1 end if end while A[p] := A[left]; A[left] := x return left
-
Consider the following set of properties. These can be used a loop invariant for all three of the loops that are included in the above code.
- p ≤ left ≤ r
- p+1 ≤ right ≤ r+1
- left ≥ right−1
- For every integer j, if p+1 ≤ j ≤ right−1 then A[j]<x
- For every integer j, if left+1 ≤ j ≤ r then A[j]≥x
Prove that the above set of properties really does form a loop invariant for each of the three loops in this code.
The trickiest part of this might be to establish that left≥right−1. To see that this inequality is always satisfied, consider a proof by contradiction: Suppose instead that left≤right−2. Then use parts (iv) and (v) of the loop invariant, considering the value of A[left+1], to obtain a contradiction.
-
Use the above loop invariant to prove that if the outer loop ever terminates then left = right−1 when this happens.
Use this information, and the fact that loop invariant still holds at this point, to establish the partial correctness of this algorithm.
-
To establish termination and bound the running time of this algorithm, consider the function
left − right + 1
Show that this is a loop variant for each of the three loops included in this program.
The trickiest part of this might be to establish that the test for each of the loops fails when the value of this expression is less than or equal to zero. It will be useful to consider the last two parts of the loop invariant (established in the first part of this question) when you consider the inner two loops.
-
Notice that the value of the loop variant is never increased by any statement inside the loops.
Use this to argue that the sum of the numbers of executions of the bodies of all three loops is at most r−p.
Conclude from this (and further inspection of the code) that the number of steps used by the entire algorithm is in O(r−p) in the worst case.
-
-
Implement the deterministic and randomized Quicksort algorithms, as well as any variations from previous questions that you are interested in, as Java programs. As usual, you should try to make your programs as general as possible.
|
This page last modified:
http://www.cpsc.ucalgary.ca/~jacobs/cpsc331/F08/tutorials/tutorial13.html |